题目内容
已知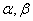 是两个不同的平面,
是两个不同的平面,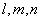 是不同的直线,下列命题不正确的是
是不同的直线,下列命题不正确的是
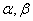 是两个不同的平面,
是两个不同的平面,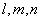 是不同的直线,下列命题不正确的是
是不同的直线,下列命题不正确的是A.若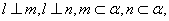 则 则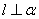 |
B.若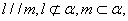 则 则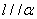 |
C.若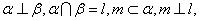 则 则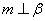 |
D.若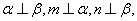 ,则 ,则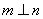 |
A ;
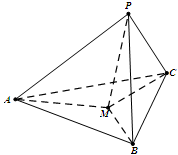
试题分析:由线面垂直的判定定理可知,一条直线垂直于平面内的两条相交直线时,該直线垂直于这个平面,因此,A不正确,选A。
点评:简单题,熟记定理是解题的关键。说明命题不正确,结合身边的模型举反例。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的棱长为1,
的棱长为1, 分别为线段
分别为线段 上的动点,则三棱锥
上的动点,则三棱锥 的体积为________.
的体积为________.
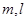 是不同的直线,
是不同的直线,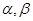 是不同的平面,给出下列五个命题:
是不同的平面,给出下列五个命题: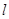 垂直于
垂直于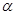 内的两条直线,则
内的两条直线,则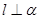 ;
;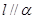 ,则
,则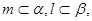 且
且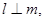 则
则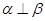 ;
;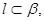 且
且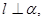 则
则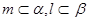 且
且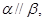 则
则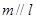 .其中正确命题的序号是
.其中正确命题的序号是  的底面是正方形,
的底面是正方形, ,点
,点 在棱
在棱 上.
上.
 平面
平面 ;
; ,且
,且 时,确定点
时,确定点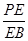 的值.
的值.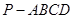 中,底面
中,底面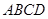 是矩形,
是矩形,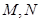 分别为
分别为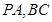 的中点,
的中点,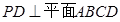 ,且
,且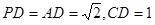
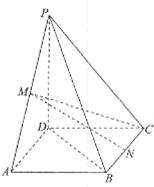
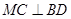 ;
;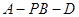 的余弦值。
的余弦值。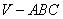 底面为正三角形,侧面
底面为正三角形,侧面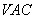 与底面垂直且
与底面垂直且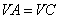 ,已知其主视图的面积为
,已知其主视图的面积为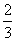 ,则其左视图的面积为
,则其左视图的面积为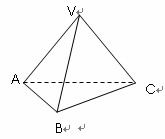
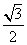

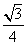
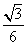
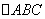 是边长为
是边长为 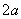 的等边三角形,
的等边三角形, 是分别以
是分别以 为底的全等的等腰三角形,现将该平面图形分别沿
为底的全等的等腰三角形,现将该平面图形分别沿 垂直,连接
垂直,连接 ,得到图二所示的几何体,据此几何体解决下面问题.
,得到图二所示的几何体,据此几何体解决下面问题.
 ;
; 时,求三棱锥
时,求三棱锥 的体积
的体积 ;
; 的余弦值.
的余弦值.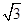 ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.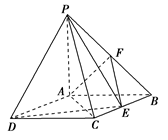
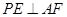 ;
;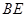 为何值时,
为何值时, 与平面
与平面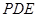 所成角的大小为45°.
所成角的大小为45°.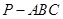 中,
中,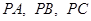 两两垂直,且
两两垂直,且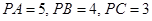 .设点
.设点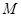 为底面
为底面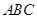 内一点,定义
内一点,定义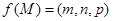 ,其中
,其中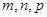 分别为三棱锥
分别为三棱锥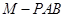 、
、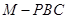 、
、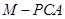 的体积.若
的体积.若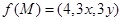 ,且
,且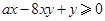 恒成立,则正实数
恒成立,则正实数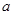 的取值范围是___________.
的取值范围是___________.