题目内容
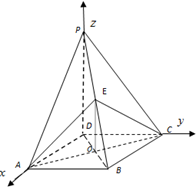
如图,四棱锥 的底面是正方形,
的底面是正方形, ,点
,点 在棱
在棱 上.
上.

(Ⅰ) 求证:平面 平面
平面 ;
;
(Ⅱ) 当 ,且
,且 时,确定点
时,确定点 的位置,即求出
的位置,即求出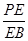 的值.
的值.
 的底面是正方形,
的底面是正方形, ,点
,点 在棱
在棱 上.
上.
(Ⅰ) 求证:平面
 平面
平面 ;
;(Ⅱ) 当
 ,且
,且 时,确定点
时,确定点 的位置,即求出
的位置,即求出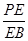 的值.
的值.(1)主要是考查了面面垂直的判定定理的运用,先证明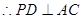 ,
,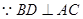
(2)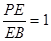
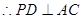 ,
,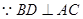
(2)
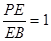
试题分析:(Ⅰ)设
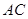 交
交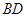 于
于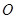 ,连接
,连接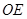
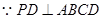 ,
,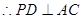 ,
,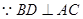
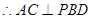 ,又
,又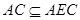 ,
,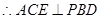 6分
6分(Ⅱ)(方法一)根据题意,由于当
 ,且
,且 时
时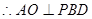
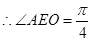 ,设
,设 ,则
,则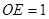 即
即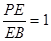 …12
…12另解:(Ⅰ)设AC交BD于O,连接OE,∵PD⊥平面ABCD,∴PD⊥AC,∵BD⊥AC,∴AC⊥平面PBD,
又∵AC⊆平面AEC,∴平面ACE⊥平面PBD.…(6分)(Ⅱ)(方法一)∵平面ACE⊥平面PBD,∴AO⊥PBD,
∵直线AE与平面PBD成角为45°,∴∠AEO=45°,设PD=
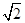 AB=2,则OE=1,∴PE:EB=1.…(12分)
AB=2,则OE=1,∴PE:EB=1.…(12分)点评:主要是考查了空间中面面垂直以及几何体的体积的公式的运用,属于中档题。

练习册系列答案
相关题目
 ,
, ,
, ,则
,则 与
与 的位置关系是( )
的位置关系是( )

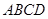 中,
中,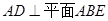 ,
,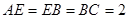 ,
, 为
为 上的点,且
上的点,且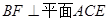 ,AC、BD交于点G.
,AC、BD交于点G.
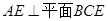 ;
; ;
; 的体积.
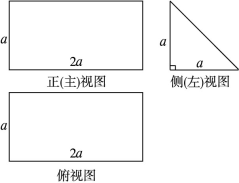
的体积.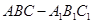 的三视图,正(主)视图和俯视图都是矩形,侧(左)视图为等边三角形,
的三视图,正(主)视图和俯视图都是矩形,侧(左)视图为等边三角形, 为
为 的中点.
的中点.
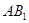 ∥平面
∥平面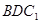 ;
;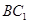 ,且
,且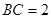 ,求点
,求点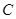 到平面
到平面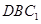 的距离.
的距离.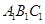 中,底面
中,底面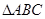 为正三角形,
为正三角形,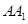
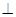 平面ABC,
平面ABC,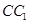 的中点,M是线段
的中点,M是线段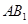 上的动点。
上的动点。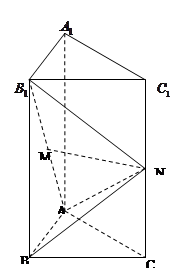
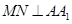 ,请给出证明;
,请给出证明;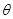 ,求
,求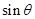 的最大值。
的最大值。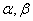 是两个不同的平面,
是两个不同的平面,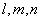 是不同的直线,下列命题不正确的是
是不同的直线,下列命题不正确的是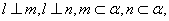 则
则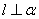
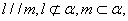 则
则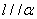
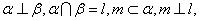 则
则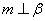
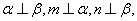 ,则
,则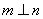
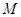 ,
,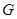 分别是
分别是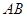 ,
,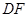 的中点.
的中点.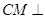 平面
平面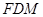 ;
;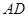 上(含
上(含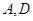 端点)确定一点
端点)确定一点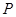 ,使得
,使得 ∥平面
∥平面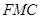 ,并给出证明.
,并给出证明.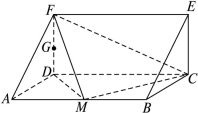
 中,
中,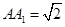 ,
,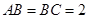 ,
,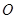 是底面对角线的交点.
是底面对角线的交点.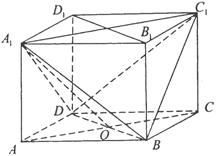
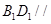 平面
平面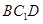 ;
;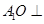 平面
平面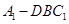 的体积。
的体积。