题目内容
5.已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为e=$\frac{1}{2}$,以原点为圆心,椭圆短半轴长为半径的圆与直径x-y+$\sqrt{6}$=0相切.(1)求椭圆C的方程;
(2)设过点(-1,0)的直线l与椭圆C相交于A,B两点,试问在x轴上是否存在一个定点M,使得$\overrightarrow{MA}•\overrightarrow{MB}$恒为定值?若存在,求出该定值及点M的坐标;若不存在,请说明理由.
分析 (1)以原点为圆心,椭圆短半袖长为半径的圆与直径x-y+$\sqrt{6}$=0相切.可得$\frac{\sqrt{6}}{\sqrt{2}}$=b,又$\frac{c}{a}=\frac{1}{2}$,a2-c2=b2,解出即可.
(2)假设在x轴上存在一个定点M(m,0),使得$\overrightarrow{MA}•\overrightarrow{MB}$恒为定值.当AB⊥x轴时,可得A$(-1,\frac{3}{2})$,B$(-1,-\frac{3}{2})$,则$\overrightarrow{MA}•\overrightarrow{MB}$=(1+m)2-$\frac{9}{4}$.当l与x轴重合时,取A(-2,0),B(2,0),$\overrightarrow{MA}•\overrightarrow{MB}$=m2-4,可得m=$-\frac{11}{8}$.定值-$\frac{135}{64}$.假设直线l的斜率存在且不为0,设直线l的方程为:y=k(x+1).A(x1,y1),B(x2,y2).与椭圆方程联立化为一元二次方程,利用根与系数的关系、数量积运算性质即可证明.
解答 解:(1)∵以原点为圆心,椭圆短半袖长为半径的圆与直径x-y+$\sqrt{6}$=0相切.
∴$\frac{\sqrt{6}}{\sqrt{2}}$=b,又$\frac{c}{a}=\frac{1}{2}$,a2-c2=b2,
解得b2=3,c=1,a=2.
∴椭圆C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.
(2)假设在x轴上存在一个定点M(m,0),使得$\overrightarrow{MA}•\overrightarrow{MB}$恒为定值.
当AB⊥x轴时,可得A$(-1,\frac{3}{2})$,B$(-1,-\frac{3}{2})$,则$\overrightarrow{MA}•\overrightarrow{MB}$=(1+m)2-$\frac{9}{4}$.
当l与x轴重合时,取A(-2,0),B(2,0),$\overrightarrow{MA}•\overrightarrow{MB}$=m2-4,
于是$\overrightarrow{MA}•\overrightarrow{MB}$=(1+m)2-$\frac{9}{4}$=m2-4,解得m=$-\frac{11}{8}$.
下面证明:在x轴上存在一个定点M(-$\frac{11}{8}$,0),使得$\overrightarrow{MA}•\overrightarrow{MB}$恒为定值-$\frac{135}{64}$.
假设直线l的斜率存在且不为0,设直线l的方程为:y=k(x+1).A(x1,y1),B(x2,y2).
联立$\left\{\begin{array}{l}{y=k(x+1)}\\{3{x}^{2}+4{y}^{2}=12}\end{array}\right.$,
化为(3+4k2)x2+8k2x+4k2-12=0,
∴x1x2=$\frac{4{k}^{2}-12}{3+4{k}^{2}}$,x1+x2=$\frac{-8{k}^{2}}{3+4{k}^{2}}$.
∴y1y2=k2(x1+1)(x2+1)=k2(x1+x2+x1x2+1).
∴$\overrightarrow{MA}•\overrightarrow{MB}$=$({x}_{1}+\frac{11}{8},{y}_{1})$•$({x}_{2}+\frac{11}{8},{y}_{2})$
=x1x2+$\frac{11}{8}({x}_{1}+{x}_{2})$+$\frac{121}{64}$+y1y2
=$\frac{4{k}^{2}-12}{3+4{k}^{2}}$+$\frac{11}{8}×\frac{-8{k}^{2}}{3+4{k}^{2}}$+$\frac{121}{64}$+${k}^{2}(\frac{4{k}^{2}-12-8{k}^{2}}{3+4{k}^{2}}+1)$
=$\frac{121}{64}$-4
=$-\frac{135}{64}$.
∴在x轴上存在一个定点M(-$\frac{11}{8}$,0),使得$\overrightarrow{MA}•\overrightarrow{MB}$恒为定值-$\frac{135}{64}$.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立化为一元二次方程的根与系数的关系、数量积运算性质、定值问题,考查了探究问题、分类讨论思想方法、推理能力与计算能力,属于难题.

 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案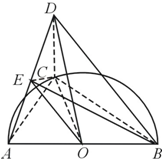 如图,已知点C是圆心为O半径为1的半圆弧上从点A数起的第一个三等分点,AB是直径,CD=1,CD⊥平面ABC,点E是AD的中点.
如图,已知点C是圆心为O半径为1的半圆弧上从点A数起的第一个三等分点,AB是直径,CD=1,CD⊥平面ABC,点E是AD的中点. 如图所示正方体ABCD-A1B1C1D1的棱长为2,线段B1D1上有两个动点E,F且EF=$\sqrt{2}$,给出下列五个结论
如图所示正方体ABCD-A1B1C1D1的棱长为2,线段B1D1上有两个动点E,F且EF=$\sqrt{2}$,给出下列五个结论