题目内容
对于定义域为D的函数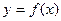 ,若同时满足下列条件:①
,若同时满足下列条件:①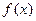 在D内单调
在D内单调
递增或单调递减;②存在区间[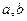 ]
]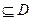 ,使
,使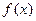 在[
在[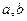 ]上的值域为[
]上的值域为[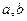 ];那么把
];那么把
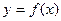 (
(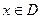 )叫闭函数。
)叫闭函数。
(1)求闭函数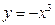 符合条件②的区间[
符合条件②的区间[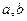 ];
];
(2)判断函数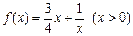 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(3)若函数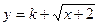 是闭函数,求实数
是闭函数,求实数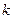 的取值范围。
的取值范围。
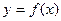 ,若同时满足下列条件:①
,若同时满足下列条件:①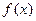 在D内单调
在D内单调递增或单调递减;②存在区间[
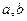 ]
]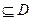 ,使
,使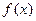 在[
在[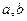 ]上的值域为[
]上的值域为[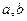 ];那么把
];那么把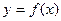 (
(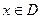 )叫闭函数。
)叫闭函数。(1)求闭函数
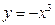 符合条件②的区间[
符合条件②的区间[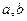 ];
];(2)判断函数
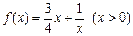 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;(3)若函数
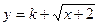 是闭函数,求实数
是闭函数,求实数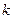 的取值范围。
的取值范围。(1)[-1,1]
(2)该函数不是闭函数
(3)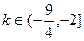
(2)该函数不是闭函数
(3)
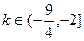
(1)由题意,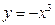 在[
在[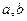 ]上递减,则
]上递减,则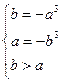 解得
解得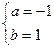
所以,所求的区间为[-1,1]
(2)取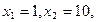 则
则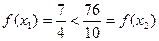 ,即
,即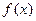 不是
不是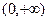 上的减函数。取
上的减函数。取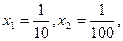
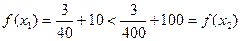 ,
,
即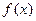 不是
不是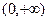 上的增函数,
上的增函数,
所以,函数在定义域内不单调递增或单调递减,从而该函数不是闭函数。
(3)若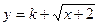 是闭函数,则存在区间[
是闭函数,则存在区间[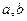 ],在区间[
],在区间[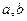 ]上,函数
]上,函数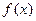 的值域为[
的值域为[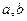 ],即
],即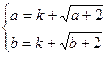 ,
,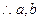 为方程
为方程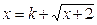 的两个实根,
的两个实根,
即方程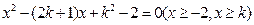 有两个不等的实根。
有两个不等的实根。
当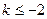 时,有
时,有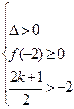 ,解得
,解得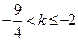 。当
。当 时,有
时,有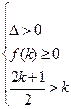 ,无解。 综上所述,
,无解。 综上所述,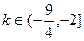 。
。
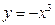 在[
在[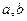 ]上递减,则
]上递减,则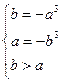 解得
解得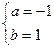
所以,所求的区间为[-1,1]
|
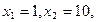 则
则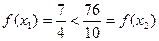 ,即
,即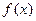 不是
不是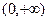 上的减函数。取
上的减函数。取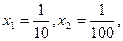
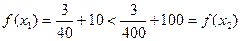 ,
,即
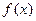 不是
不是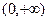 上的增函数,
上的增函数,所以,函数在定义域内不单调递增或单调递减,从而该函数不是闭函数。
(3)若
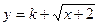 是闭函数,则存在区间[
是闭函数,则存在区间[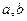 ],在区间[
],在区间[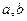 ]上,函数
]上,函数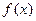 的值域为[
的值域为[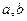 ],即
],即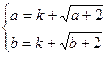 ,
,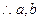 为方程
为方程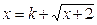 的两个实根,
的两个实根,即方程
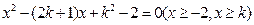 有两个不等的实根。
有两个不等的实根。当
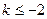 时,有
时,有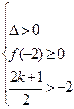 ,解得
,解得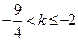 。当
。当 时,有
时,有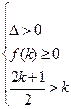 ,无解。 综上所述,
,无解。 综上所述,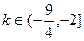 。
。
练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 ,其中
,其中 .⑴若
.⑴若 的定义域为区间
的定义域为区间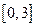 ,求
,求 的最
的最 ,求
,求 的取值范围,使
的取值范围,使 在定义域
在定义域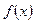 同时满足:①对于定义域上的任意
同时满足:①对于定义域上的任意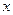 ,恒有
,恒有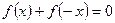
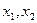 ,当
,当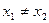 时,恒有
时,恒有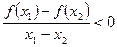 ,则称函数
,则称函数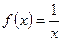 ,⑵
,⑵ 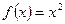 ,⑶
,⑶ 
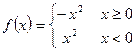 ,能被称为“理想函数”的有 (填相应的序号)
,能被称为“理想函数”的有 (填相应的序号) ,
, ,则
,则 的图象的交点个数为 个
的图象的交点个数为 个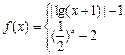
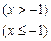 ,则函数的零点的个数有 个。
,则函数的零点的个数有 个。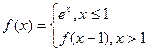 ,则
,则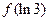 =" " ( )
=" " ( )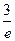
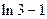
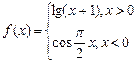 图象上关于坐标原点
图象上关于坐标原点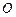 对称的点有
对称的点有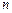 对,则
对,则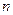 的值有( )
的值有( )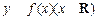 满足
满足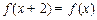 ,且当
,且当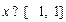 时,
时,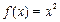 ,则
,则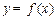 与
与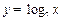 的图象的交点个数为( )
的图象的交点个数为( )