题目内容
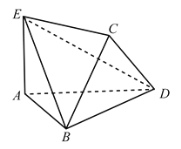
【题目】如图,四边形![]() 为正方形,
为正方形,![]() 平面
平面![]() ,
,![]() ,
,![]() .
.
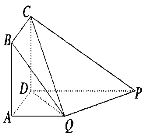
(1)证明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析.(2)![]()
【解析】
以![]() 为坐标原点,线段
为坐标原点,线段![]() 的长为单位长,射线
的长为单位长,射线![]() 为
为![]() 轴的正半轴建立空间直角坐标系
轴的正半轴建立空间直角坐标系![]() .
.
(1)求出相应点的坐标,根据线面垂直的判断定理、面面垂直的判定定理,结合空间向量数量积的坐标运算公式进行证明即可;
(2)利用空间向量夹角公式,结合平面法向量的求法进行求解即可.
如图,
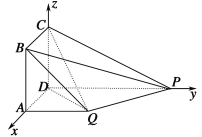
以![]() 为坐标原点,线段
为坐标原点,线段![]() 的长为单位长,射线
的长为单位长,射线![]() 为
为![]() 轴的正半轴建立空间直角坐标系
轴的正半轴建立空间直角坐标系![]() .
.
(1)证明:依题意有![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() .
.
即![]() ,
,![]() .
.
故![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
(2)依题意有![]() ,
,![]() ,
,![]() .
.
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则
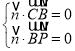 ,即
,即![]() .
.
因此可取![]() .
.
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则
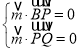 ,可取
,可取![]() ,所以
,所以![]() .
.
故二面角![]() 的余弦值为
的余弦值为![]() .
.

【题目】某网购平台为了解某市居民在该平台的消费情况,从该市使用其平台且每周平均消费额超过100元的人员中随机抽取了100名,并绘制如图所示频率分布直方图,已知中间三组的人数可构成等差数列.
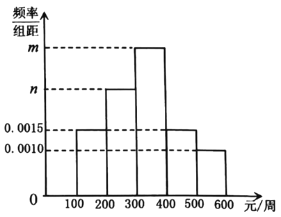
(1)求![]() 的值;
的值;
(2)分析人员对100名调查对象的性别进行统计发现,消费金额不低于300元的男性有20人,低于300元的男性有25人,根据统计数据完成下列![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为消费金额与性别有关?
的把握认为消费金额与性别有关?
(3)分析人员对抽取对象每周的消费金额![]() 与年龄
与年龄![]() 进一步分析,发现他们线性相关,得到回归方程
进一步分析,发现他们线性相关,得到回归方程![]() .已知100名使用者的平均年龄为38岁,试判断一名年龄为25岁的年轻人每周的平均消费金额为多少.(同一组数据用该区间的中点值代替)
.已知100名使用者的平均年龄为38岁,试判断一名年龄为25岁的年轻人每周的平均消费金额为多少.(同一组数据用该区间的中点值代替)
![]() 列联表
列联表
男性 | 女性 | 合计 | |
消费金额 | |||
消费金额 | |||
合计 |
临界值表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]() ,其中
,其中![]()
【题目】为了丰富学生的课外文化生活,某中学积极探索开展课外文体活动的新途径及新形式,取得了良好的效果.为了调查学生的学习积极性与参加文体活动是否有关,学校对300名学生做了问卷调查,列联表如下:
参加文体活动 | 不参加文体活动 | 合计 | |
学习积极性高 | 180 | ||
学习积极性不高 | 60 | ||
合计 | 300 |
已知在全部300人中随机抽取1人,抽到学习积极性不高的学生的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有![]() 的把握认为学习积极性高与参加文体活动有关?请说明你的理由;
的把握认为学习积极性高与参加文体活动有关?请说明你的理由;
(3)若从不参加文体活动的同学中按照分层抽样的方法选取5人,再从所选出的5人中随机选取2人,求至少有1人学习积极性不高的概率.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() ,其中
,其中![]() .
.
【题目】某中药种植基地有两处种植区的药材需在下周一、下周二两天内采摘完毕,基地员工一天可以完成一处种植区的采摘.由于下雨会影响药材品质,基地收益如下表所示:
周一 | 无雨 | 无雨 | 有雨 | 有雨 |
周二 | 无雨 | 有雨 | 无雨 | 有雨 |
收益 |
|
|
|
|
若基地额外聘请工人,可在周一当天完成全部采摘任务.无雨时收益为![]() 万元;有雨时,收益为
万元;有雨时,收益为![]() 万元.额外聘请工人的成本为
万元.额外聘请工人的成本为![]() 万元.
万元.
已知下周一和下周二有雨的概率相同,两天是否下雨互不影响,基地收益为![]() 万元的概率为
万元的概率为![]() .
.
(Ⅰ)若不额外聘请工人,写出基地收益![]() 的分布列及基地的预期收益;
的分布列及基地的预期收益;
(Ⅱ)该基地是否应该外聘工人,请说明理由.