题目内容
已知函数 满足:①定义在
满足:①定义在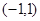 上;②当
上;②当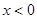 时,
时,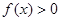 ;③对于任意的
;③对于任意的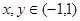 ,有
,有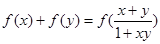 .
.
(1)取一个对数函数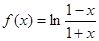 ,验证它是否满足条件②,③;
,验证它是否满足条件②,③;
(2)对于满足条件①,②,③的一般函数 ,判断
,判断 是否具有奇偶性和单调性,并加以证明.
是否具有奇偶性和单调性,并加以证明.
 满足:①定义在
满足:①定义在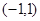 上;②当
上;②当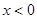 时,
时,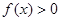 ;③对于任意的
;③对于任意的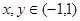 ,有
,有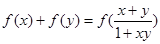 .
.(1)取一个对数函数
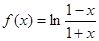 ,验证它是否满足条件②,③;
,验证它是否满足条件②,③; (2)对于满足条件①,②,③的一般函数
 ,判断
,判断 是否具有奇偶性和单调性,并加以证明.
是否具有奇偶性和单调性,并加以证明. (1)当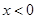 时,
时,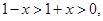
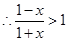
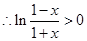 .
.
又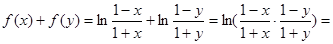
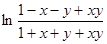
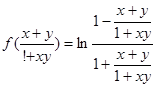
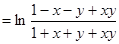 ,即
,即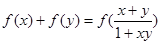 .
.
故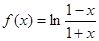 满足条件②,③.
满足条件②,③.
(2) 在
在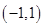 上是奇函数.
上是奇函数.  在
在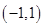 上是减函数.
上是减函数.
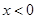 时,
时,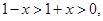
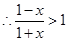
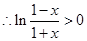 .
.又
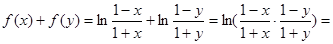
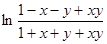
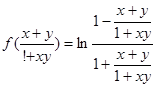
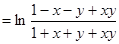 ,即
,即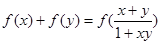 .
.故
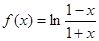 满足条件②,③.
满足条件②,③.(2)
 在
在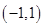 上是奇函数.
上是奇函数.  在
在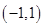 上是减函数.
上是减函数.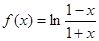 ,当
,当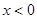 ,时先计算出
,时先计算出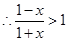 ,在利用对数函数的性质,得
,在利用对数函数的性质,得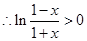 ;利用对数的运算法则,得出
;利用对数的运算法则,得出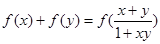 。
。解:(1)当
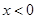 时,
时,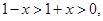
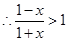
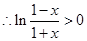 .
.又
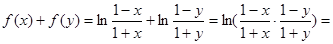
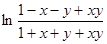
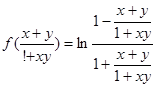
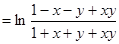 ,即
,即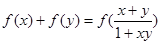 .
.故
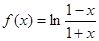 满足条件②,③.
满足条件②,③.(2)这样的函数是奇函数.
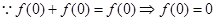
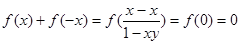
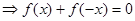
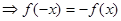
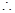
 在
在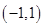 上是奇函数.
上是奇函数.这样的函数是减函数.
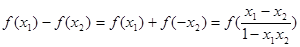
当
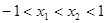 时,
时,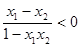 ,由条件知
,由条件知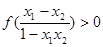 ,即
,即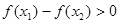 .
.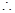
 在
在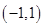 上是减函数.
上是减函数.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
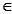 R,函数
R,函数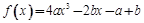 .
.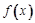 的最大值为|2a-b|﹢a;
的最大值为|2a-b|﹢a;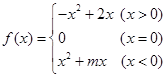 为奇函数,若函数
为奇函数,若函数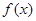 在区间
在区间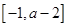 上单调递增,则
上单调递增,则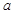 的取值范围是
的取值范围是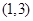
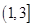
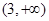
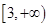
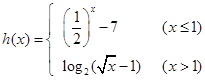
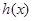 在区间
在区间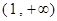 上的单调性并用定义证明;
上的单调性并用定义证明;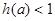 ,求
,求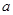 的取值范围.
的取值范围.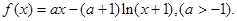
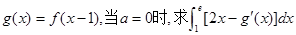 ;
;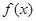 的单调区间;
的单调区间;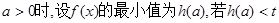 恒成立,求实数t的取值范围。
恒成立,求实数t的取值范围。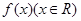 满足:
满足: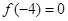 ,且在区间
,且在区间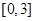 与
与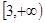 上分别递减和递增,则不等式
上分别递减和递增,则不等式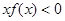 的解集为_____.
的解集为_____.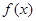 的图像关于
的图像关于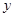 轴对称,又已知
轴对称,又已知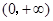 上为减函数,且
上为减函数,且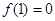 ,则不等式
,则不等式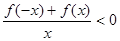 的解集为( )
的解集为( )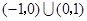
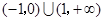
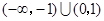
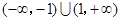
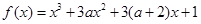 有极大值和极小值,则
有极大值和极小值,则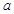 的取值范围是( )
的取值范围是( )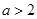 或
或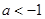
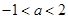
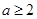 或
或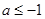
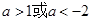
 求函数
求函数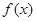 的最大值和最小值.
的最大值和最小值.