题目内容
若棱长为1的正方体ABCD-A1B1C1D1 的八个顶点都在球O的表面上,则A,A1两点之间的球面距离为
arccos
arccos
.
| ||
| 2 |
| 1 |
| 3 |
| ||
| 2 |
| 1 |
| 3 |
分析:由已知中棱长为1的正方体ABCD-A1B1C1D1 的八个顶点都在球O的表面上,我们可以求出球O的半径,进而根据AA1,解三角形AOA1,求出∠AOA1的大小,进而根据弧长公式,即可求出答案.
解答:解:∵棱长为1的正方体ABCD-A1B1C1D1 的八个顶点都在球O的表面上,
故球O的直径等于正方体的对角线长
即2R=
∴R=
又∵AA1=1
∴∠AOA1=arccos
则A,A1两点之间的球面距离为
arccos
故答案为:
arccos
故球O的直径等于正方体的对角线长
即2R=
| 3 |
∴R=
| ||
| 2 |
又∵AA1=1
∴∠AOA1=arccos
| 1 |
| 3 |
则A,A1两点之间的球面距离为
| ||
| 2 |
| 1 |
| 3 |
故答案为:
| ||
| 2 |
| 1 |
| 3 |
点评:本题考查的知识点是球内接多面体,弧长公式,其中根据已知条件求出球的关径,及弧AA1对应的圆心角的度数是解答本题的关键.

练习册系列答案
相关题目
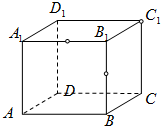 在棱长为1的正方体ABCD-A1B1C1D1的密闭容器中,棱A1B1和棱BB1的中点处各有一个小孔,顶点C1处也有一个小孔,若正方体可任意放置,且小孔面积不计,则这个正方体容器中最多可容纳水的体积是( )
在棱长为1的正方体ABCD-A1B1C1D1的密闭容器中,棱A1B1和棱BB1的中点处各有一个小孔,顶点C1处也有一个小孔,若正方体可任意放置,且小孔面积不计,则这个正方体容器中最多可容纳水的体积是( )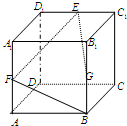 在棱长为1的正方体ABCD-A1B1C1D1中,若E,F,G分别为C1D1,AA1,BB1的中点,则空间四边形EFBG在正方体下底面ABCD上的射影面积为( )
在棱长为1的正方体ABCD-A1B1C1D1中,若E,F,G分别为C1D1,AA1,BB1的中点,则空间四边形EFBG在正方体下底面ABCD上的射影面积为( ) 已知棱长为1的正方体容器ABCD-A1B1C1D1,在棱AB,BB1以及BC1的中点处各有一个小孔E、F、G,若此容器可以任意放置,则该容器可装水的最大容积为( )
已知棱长为1的正方体容器ABCD-A1B1C1D1,在棱AB,BB1以及BC1的中点处各有一个小孔E、F、G,若此容器可以任意放置,则该容器可装水的最大容积为( )