Question

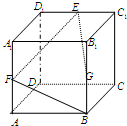在棱长为1的正方体ABCD-A₁B₁C₁D₁中，若E，F，G分别为C₁D₁，AA₁，BB₁的中点，则空间四边形EFBG在正方体下底面ABCD上的射影面积为（　　）

• A、1
• B、

  1

  2

• C、

  1

  4

• D、

  5

  8

Answer 1

分析：过E点做EH垂直CD于H，连接EH，易得H即为E在平面ABCD上的射影，连接AH，BH，可得△ABH即为空间四边形EFBG在正方体下底面ABCD上的射影，求出△ABH的面积，即可得到答案．

解答：解：过E点做EH垂直CD于H，连接EH，易得H即为E在平面ABCD上的射影，
连接AH，BH，如下图所示

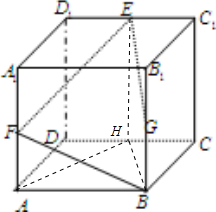
则AH，BH，AB分别为FE，EG，FB在平面ABCD上的射影，
又由G在平面ABCD上的射影为B，
故△ABH即为空间四边形EFBG在正方体下底面ABCD上的射影
∵S_△ABH=

1

2

S_ABCD=

1

2

故选B

点评：本题考查的知识点是棱柱的结构特征，其中根据正方体的结构特征，分析出△ABH即为空间四边形EFBG在正方体下底面ABCD上的射影，是解答本题的关键．