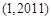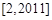题目内容
已知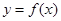 的定义域为
的定义域为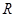 ,且恒有等式
,且恒有等式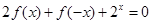 对任意的实
对任意的实
数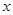 成立.
成立.
(Ⅰ)试求 的解析式;
的解析式;
(Ⅱ)讨论 在
在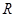 上的单调性,并用单调性定义予以证明.
上的单调性,并用单调性定义予以证明.
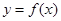 的定义域为
的定义域为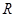 ,且恒有等式
,且恒有等式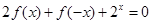 对任意的实
对任意的实数
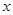 成立.
成立.(Ⅰ)试求
 的解析式;
的解析式;(Ⅱ)讨论
 在
在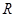 上的单调性,并用单调性定义予以证明.
上的单调性,并用单调性定义予以证明. (Ⅰ)f(x)=[2^(-x)-2^(x+1)]/3
(Ⅱ)函数在R上为减函数,证明见解析。
(Ⅱ)函数在R上为减函数,证明见解析。
本试题主要是考查了求解函数的解析式,以及函数单调性的证明。
(1)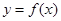 的定义域为
的定义域为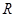 ,且恒有等式
,且恒有等式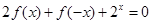 对任意的实数
对任意的实数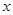 成立.,那么可以得到方程组,消元法得到结论。
成立.,那么可以得到方程组,消元法得到结论。
(2)设出变量,运用定义法证明单调性。
解:
1、2f(x)+f(-x)+2^x=0 …………1
2f(-x)+f(x)+2^(-x)=0 …………2
1式X2-2式得:
3f(x)+2^(x+1)-2^(-x)=0
即:f(x)=[2^(-x)-2^(x+1)]/3
2、设x1<x2 可得:
f(x1)-f(x2)
=[2^(-x1)-2^(x1+1)]/3-[2^(-x2)-2^(x2+1)]/3
=[2^(-x1)-2^(-x2)]/3+[2^(x2+1)-2^(x1+1)]/3
因:x1<x2 所以有:-x1>-x2 ,x1+1<x2+1
所以:2^(-x1)>2^(-x2)
2^(x2+1)>2^(x1+1)
即:f(x1)-f(x2)>0
所以此函数在R上为减函数!
(1)
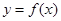 的定义域为
的定义域为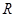 ,且恒有等式
,且恒有等式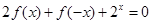 对任意的实数
对任意的实数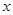 成立.,那么可以得到方程组,消元法得到结论。
成立.,那么可以得到方程组,消元法得到结论。(2)设出变量,运用定义法证明单调性。
解:
1、2f(x)+f(-x)+2^x=0 …………1
2f(-x)+f(x)+2^(-x)=0 …………2
1式X2-2式得:
3f(x)+2^(x+1)-2^(-x)=0
即:f(x)=[2^(-x)-2^(x+1)]/3
2、设x1<x2 可得:
f(x1)-f(x2)
=[2^(-x1)-2^(x1+1)]/3-[2^(-x2)-2^(x2+1)]/3
=[2^(-x1)-2^(-x2)]/3+[2^(x2+1)-2^(x1+1)]/3
因:x1<x2 所以有:-x1>-x2 ,x1+1<x2+1
所以:2^(-x1)>2^(-x2)
2^(x2+1)>2^(x1+1)
即:f(x1)-f(x2)>0
所以此函数在R上为减函数!

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 +4x+3,g(x)为一次函数,若f(g(x))=x
+4x+3,g(x)为一次函数,若f(g(x))=x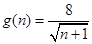 (
(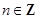 且n≥0),若产品销售价保持不变,第n次投入后的年利润为
且n≥0),若产品销售价保持不变,第n次投入后的年利润为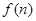 万元.
万元.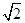 ,+∞)
,+∞) 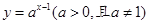 的图象恒过定点A,若点A在一次函数
的图象恒过定点A,若点A在一次函数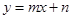 的图象上,其中
的图象上,其中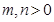 ,则
,则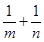 的最小值为 .
的最小值为 .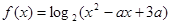 在[2,+
在[2,+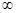 )上是增函数,则
)上是增函数,则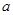 的取值范围
的取值范围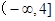
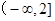
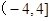
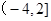
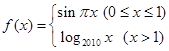 ,若
,若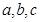 互不相等,且
互不相等,且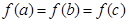 ,
,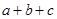 的取值范围是( )
的取值范围是( )