题目内容
10.将函数y=$\sqrt{3}$sin2x-2sin2x的图象沿x轴向右平移a(a>0)个单位长度,所得函数的图象关于y轴对称,则a的最小值是$\frac{π}{3}$.分析 利用三角函数的恒等变换化简函数的解析式,再利用函数y=Asin(ωx+φ)的图象变换规律,正弦函数、余弦函数的图象的对称性,可得-2a+$\frac{π}{6}$=kπ+$\frac{π}{2}$,k∈Z,由此求得a的最小值.
解答 解:将函数y=$\sqrt{3}$sin2x-2sin2x=$\sqrt{3}$sin2x+cos2x-1=2sin(2x+$\frac{π}{6}$)-1的图象沿x轴向右平移a(a>0)个单位长度,
可得y=2sin[2(x-a)+$\frac{π}{6}$]-1=2sin(2x-2a+$\frac{π}{6}$)-1的图象;
再根据所得函数的图象关于y轴对称,可得-2a+$\frac{π}{6}$=kπ+$\frac{π}{2}$,k∈Z,则a=-$\frac{kπ}{2}$-$\frac{π}{6}$,故a的最小值是$\frac{π}{3}$,
故答案为:$\frac{π}{3}$.
点评 本题主要考查三角函数的恒等变换,函数y=Asin(ωx+φ)的图象变换规律,正弦函数、余弦函数的图象的对称性,属于基础题.

练习册系列答案
相关题目
1.设函数f(x)=2x,则如图所示的函数图象( )
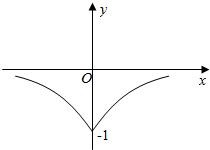

| A. | y=f(|x|) | B. | y=-|f(x)| | C. | y=-f(-|x|) | D. | y=f(-|x|) |
18.已知数据x1,x2,x3,…,xn是武汉市n(n≥3,n∈N*)个普通职工的2014年的年收入,设这n个数据的中位数为x,平均数为y,方差为z,如果再加上比尔.盖茨的2014年的年收入xn+1(约80亿美元),则这n+1个数据中,下列说法正确的是( )
| A. | 年收入平均数大大增大,中位数一定变大,方差可能不变 | |
| B. | 年收入平均数大大增大,中位数可能不变,方差变大 | |
| C. | 年收入平均数大大增大,中位数可能不变,方差也不变 | |
| D. | 年收入平均数可能不变,中位数可能不变,方差可能不变 |
5.已知函数f(x)=Asin(ωx+φ)(A≠0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)关于直线x=$\frac{2π}{3}$对称,且它的最小正周期为π,则( )
| A. | f(x)的图象过点(0,$\frac{1}{2}$) | B. | f(x)在[$\frac{π}{12}$,$\frac{2π}{3}$]上是减函数 | ||
| C. | f(x)的一个对称中心是($\frac{5π}{12}$,0) | D. | f(x)的图象的一条对称轴是x=$\frac{5π}{12}$ |
15.设函数f(x)=${(\frac{1}{2})}^{lnx}$-|lnx-2|的所有零点之积为m,则m所在的区间为( )
| A. | (1,e) | B. | (e,e2) | C. | (e2,e3) | D. | (e3,e4) |