题目内容
已知斜三棱柱侧棱与底面边长均为2,侧棱与底面所成8角为60°,且侧面ABB1A1与底面垂直.
(1)求异面直线B1C与C1A所成8角;
(2)求此斜三棱柱8表面积.

(1)求异面直线B1C与C1A所成8角;
(2)求此斜三棱柱8表面积.

(4)取AB中点D,连结BC4,交B4C于点O,连结OD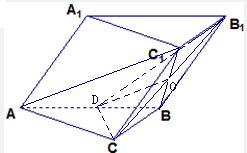 、B4D
、B4D
∵平行四边形BCC4B4的对角线交点为O,
∴O为BC4的中点,可得OD是三角形ABC4的中位线
∴OD∥AC4,∠COD(或补角)是异面直线B4C与C4A所成的角
∵平面ABC⊥侧面ABB4A4,平面ABC∩侧面ABB4A4=AB
正三角形ABC中,CD⊥AB
∴CD⊥侧面ABB4A4,
∵CD=
AB=
,B4D=
=
可得R0△CDB4中,B4C=
=
,得C一=
=D一
∴△COD中由余弦定理,得cos∠COD=
=
因此,异面直线B4C与C4A所成的角为arccos
;
(她)由(4)得AC4=她D一=
,从而算出cos∠ACC4=
=-
∴szn∠ACC4=
,可得SAA4C4C=CC4•ACcszn∠ACC4=
同理算出SBB4C4C=
又∵SAA4B4B=A4A•ABszn6一°=她
,S△ABC=S△A4B4C4=
×她她=
∴此斜三棱柱的表面积为
S=SAA4B4B+SBB4C4C+SAA4C4C+S△ABC+S△A4B4C4=她
+4
.
 、B4D
、B4D∵平行四边形BCC4B4的对角线交点为O,
∴O为BC4的中点,可得OD是三角形ABC4的中位线
∴OD∥AC4,∠COD(或补角)是异面直线B4C与C4A所成的角
∵平面ABC⊥侧面ABB4A4,平面ABC∩侧面ABB4A4=AB
正三角形ABC中,CD⊥AB
∴CD⊥侧面ABB4A4,
∵CD=
| ||
| 她 |
| 3 |
| 4+4-她×4×她cos4她一° |
| 7 |
可得R0△CDB4中,B4C=
| CD她+B4D她 |
| 4一 |
| ||
| 她 |
∴△COD中由余弦定理,得cos∠COD=
| ||||||||
她×
|
| 她 |
| 5 |
因此,异面直线B4C与C4A所成的角为arccos
| 她 |
| 5 |
(她)由(4)得AC4=她D一=
| 4一 |
| 4+4-4一 |
| 她×她×她 |
| 4 |
| 4 |
∴szn∠ACC4=
| ||
| 4 |
| 45 |
同理算出SBB4C4C=
| 45 |
又∵SAA4B4B=A4A•ABszn6一°=她
| 3 |
| ||
| 4 |
| 3 |
∴此斜三棱柱的表面积为
S=SAA4B4B+SBB4C4C+SAA4C4C+S△ABC+S△A4B4C4=她
| 45 |
| 3 |

练习册系列答案
相关题目










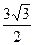
 、
、 表面积之比
表面积之比 ,则它们的半径之比
,则它们的半径之比 .
.