题目内容
已知如图,平行四边形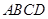 中,
中,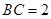 ,
,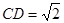 ,
,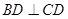 ,正方形
,正方形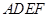 所在平面与平面
所在平面与平面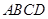 垂直,
垂直,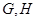 分别是
分别是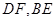 的中点。
的中点。
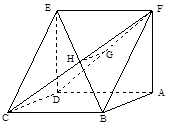
⑴求证: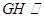 平面
平面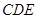 ;
;
⑵求平面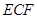 与平面
与平面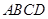 所成的二面角的正弦值。
所成的二面角的正弦值。
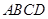 中,
中,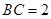 ,
,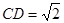 ,
,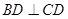 ,正方形
,正方形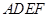 所在平面与平面
所在平面与平面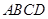 垂直,
垂直,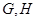 分别是
分别是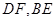 的中点。
的中点。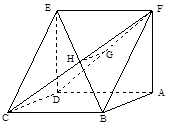
⑴求证:
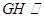 平面
平面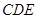 ;
;⑵求平面
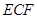 与平面
与平面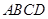 所成的二面角的正弦值。
所成的二面角的正弦值。(1)详见解析;(2)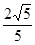 .
.
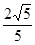 .
.试题分析:(1)证明线面平行,一般可考虑线面平行的判定定理,构造面外线平行于面内线,其手段一般是构造平行四边形,或构造三角形中位线(特别是有中点时),由此本题即要证明
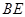 的中点
的中点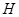 也是
也是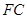 的中点,于是只要证明四边形
的中点,于是只要证明四边形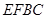 是平行四边形,此较为容易;(2)求二面角一般分为三个步骤:作出二面角的平面角,证明此角是二面角的平面角,利用解三角形知识求出二面角的三角函数值,也可建立空间直角坐标系,求出两平面的法向量的夹角,根进一步判断二面角的大小.
是平行四边形,此较为容易;(2)求二面角一般分为三个步骤:作出二面角的平面角,证明此角是二面角的平面角,利用解三角形知识求出二面角的三角函数值,也可建立空间直角坐标系,求出两平面的法向量的夹角,根进一步判断二面角的大小. 试题解析:⑴证明;
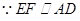 ,
,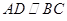 ,
,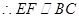 且
且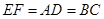 ,
, 四边形
四边形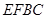 是平行四边形,
是平行四边形,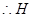 为
为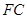 的中点,又
的中点,又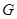 是
是 的中点
的中点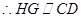 ,
,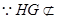 平面
平面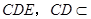 平面
平面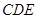 ,
,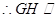 平面
平面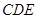 4分
4分⑵(解法1)过点
 作
作 于
于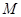 ,易知
,易知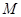 为
为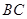 中点,连结
中点,连结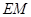 .
.易知
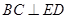 ,
,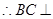 平面
平面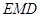 ,
,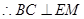 ,
,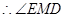 是平面
是平面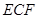 与平面
与平面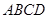 所成的二面角的平面角. 8分
所成的二面角的平面角. 8分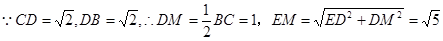 ,
,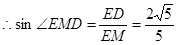 ,
,即平面
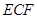 与平面
与平面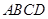 所成的二面角的正弦值为
所成的二面角的正弦值为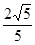 . 12分
. 12分(解法2)以点
 为坐标原点,
为坐标原点,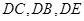 所在的直线分别为
所在的直线分别为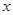 轴,
轴,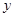 轴,
轴,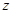 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则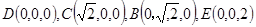 , 6分
, 6分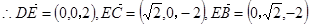 ,
,设平面
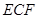 的法向量
的法向量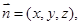 由
由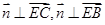 ,得
,得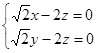 ,
,令
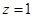 ,
,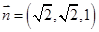 又平面
又平面 的法向量为
的法向量为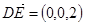 , 9分
, 9分设平面
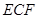 与平面
与平面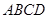 所成的二面角为
所成的二面角为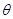 ,则
,则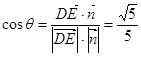 ,
,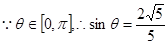
即平面
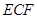 与平面
与平面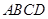 所成的二面角的正弦值为
所成的二面角的正弦值为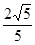 . 12分
. 12分
练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
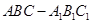 中,
中,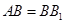 ,
,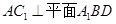 ,
, 为的
为的 中点.
中点.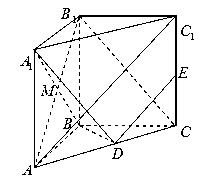
 ∥平面
∥平面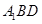 ;
;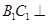 平面
平面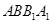 ;
;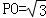 ,E、F分别是BC、AP的中点.
,E、F分别是BC、AP的中点.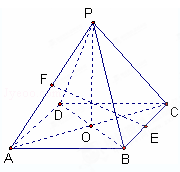
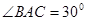 ,
,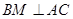 交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1,
交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1,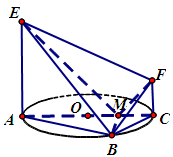
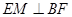 ;
;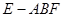 的体积
的体积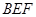 和平面
和平面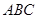 所成的锐二面角的正切值.
所成的锐二面角的正切值.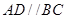 ,
,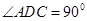 ,平面
,平面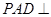 底面
底面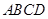 ,
,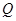 为
为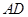 中点,M是棱PC上的点,
中点,M是棱PC上的点,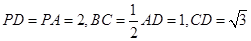 .
.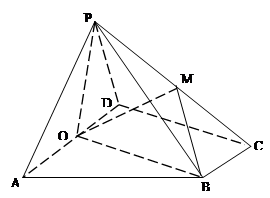
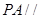 平面
平面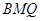 ;
;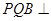 底面
底面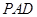 ;
; ,设PM=tMC,试确定t的值.
,设PM=tMC,试确定t的值.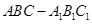 中,
中,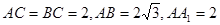 ,点
,点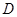 是
是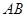 的中点.
的中点.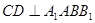 ;
;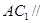 平面
平面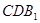 ;
;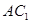 与
与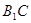 所成角的余弦值.
所成角的余弦值.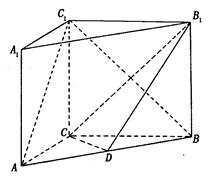
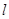 为直线,
为直线,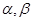 是两个不同的平面,下列命题中正确的是( )
是两个不同的平面,下列命题中正确的是( )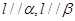 ,则
,则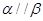
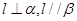 ,则
,则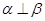
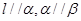 ,则
,则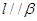
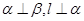 ,则
,则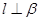
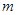 ,
,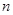 和一个平面
和一个平面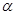 ,下列命题中的真命题是( )
,下列命题中的真命题是( )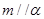 ,
, ,则
,则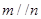
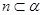 ,则
,则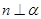 ,则
,则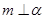 ,
, 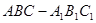 中,
中,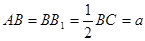 ,
,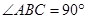 ,
,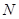 、
、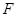 分别为
分别为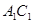 、
、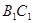 的中点.
的中点.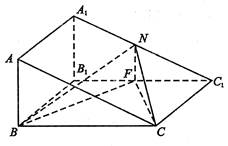
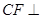 平面
平面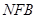 ;
;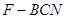 的体积.
的体积.