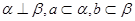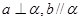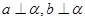题目内容
对于空间的两条直线 ,
,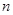 和一个平面
和一个平面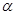 ,下列命题中的真命题是( )
,下列命题中的真命题是( )
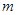 ,
,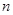 和一个平面
和一个平面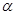 ,下列命题中的真命题是( )
,下列命题中的真命题是( )A.若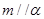 , , ,则 ,则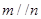 | B.若 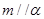 , ,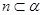 ,则 ,则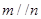 |
C.若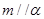 , ,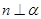 ,则 ,则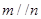 | D.若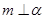 , , 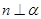 ,则 ,则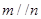 |
D
试题分析:对于A选项里面的
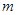 ,
,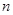 可能相交,也可能异面;对于B选项
可能相交,也可能异面;对于B选项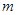 ,
,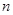 可能是异面直线;对于C选项
可能是异面直线;对于C选项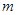 ,
,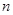 可能相交,也可能异面;选项D根据直线和平面垂直的性质定理可知正确.
可能相交,也可能异面;选项D根据直线和平面垂直的性质定理可知正确.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
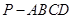 中,底面
中,底面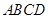 为菱形,
为菱形,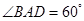 ,
,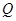 为
为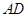 的中点.
的中点.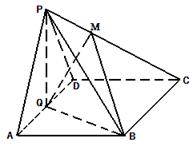
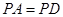 ,求证:平面
,求证:平面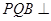 平面
平面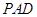 ;
;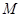 在线段
在线段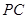 上,
上,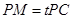 ,试确定
,试确定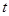 的值,使
的值,使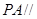 平面
平面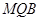 .
.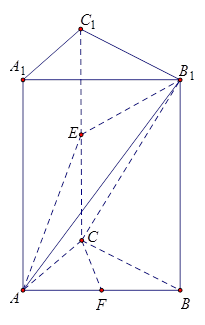
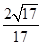 ,若存在,求CE的长,若不存在,请说明理由.
,若存在,求CE的长,若不存在,请说明理由. 中,
中,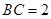 ,
,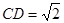 ,
,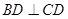 ,正方形
,正方形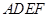 所在平面与平面
所在平面与平面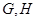 分别是
分别是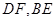 的中点。
的中点。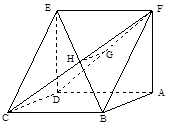
 平面
平面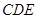 ;
;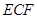 与平面
与平面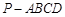 的底面是直角梯形,
的底面是直角梯形,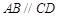 ,
,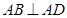 ,
,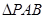 和
和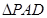 是两个边长为
是两个边长为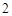 的正三角形,
的正三角形,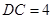 ,
, 为
为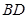 的中点,
的中点,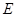 为
为 的中点.
的中点.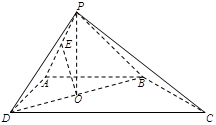
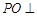 平面
平面 ;
;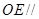 平面
平面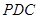 ;
;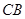 与平面
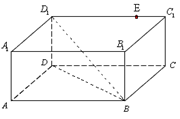
与平面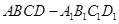 中,底面
中,底面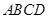 为正方形,
为正方形,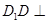 面
面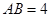 ,
,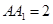 ,点
,点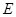 在棱
在棱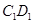 上,且
上,且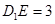 .
.
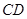 上确定一点
上确定一点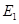 ,使得直线
,使得直线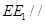 平面
平面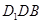 ,并证明;
,并证明;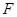 在底面
在底面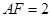 ,请说明点
,请说明点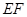 长度的最小值.
长度的最小值.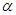 与平面
与平面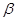 平行的是( )
平行的是( )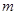 、
、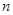 是两条不同的直线,
是两条不同的直线,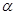 、
、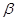 是两个不同的平面,则下面命题中正确的是( )
是两个不同的平面,则下面命题中正确的是( )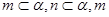 ∥
∥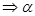 ∥
∥ ,
,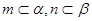
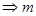 ∥
∥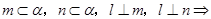
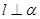
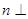
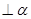
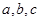 是三条不同的直线,
是三条不同的直线,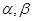 是两个不同的平面,则能使
是两个不同的平面,则能使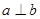 成立是( )
成立是( )