题目内容
在△ABC中,a,b,c分别是角A,B,C的对边,向量m=(2sinB,2-cos2B),n=(2sin2( +
+ ),-1),且m⊥n.
),-1),且m⊥n.
(1)求角B的大小;
(2)求sinA+cosC的取值范围.
 +
+ ),-1),且m⊥n.
),-1),且m⊥n.(1)求角B的大小;
(2)求sinA+cosC的取值范围.
(1)B= 或B=
或B=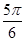
(2)(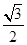 ,
,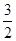 )
)
 或B=
或B=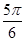
(2)(
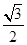 ,
,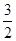 )
)解:(1)因为m⊥n,所以m·n=0,
所以2sinB·2sin2( +
+ )-2+cos2B=0,
)-2+cos2B=0,
即2sinB·[1-cos2( +
+ )]-2+cos2B=0,
)]-2+cos2B=0,
即2sinB+2sin2B-2+1-2sin2B=0,解得sinB=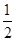 .
.
由于0<B<π,所以B= 或B=
或B=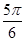 .
.
(2)当B= 时,sinA+cosC=sinA+cos(
时,sinA+cosC=sinA+cos(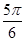 -A)=sinA-
-A)=sinA-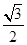 cosA+
cosA+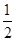 sinA=
sinA=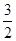 sinA-
sinA-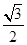 cosA=
cosA=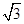 ×(
×(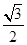 sinA-
sinA-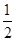 cosA)=
cosA)=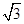 sin(A-
sin(A- ).
).
由于0<A<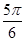 ,所以-
,所以- <A-
<A- <
<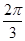 ,
,
所以-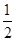 <sin(A-
<sin(A- )≤1,
)≤1,
所以sinA+cosC的取值范围是(-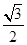 ,
,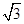 ];
];
当B=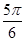 时,sinA+cosC=sinA+cos(
时,sinA+cosC=sinA+cos( -A)=sinA+
-A)=sinA+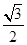 cosA+
cosA+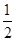 sinA=
sinA=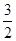 sinA+
sinA+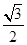 cosA=
cosA=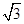 ×(
×(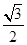 sinA+
sinA+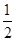 cosA)=
cosA)=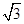 sin(A+
sin(A+ ),
),
由于0<A< ,故
,故 <A+
<A+ <
<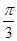 ,
,
故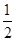 <sin(A+
<sin(A+ )<
)<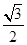 ,
,
所以sinA+cosC的取值范围是(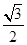 ,
,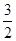 ).
).
所以2sinB·2sin2(
 +
+ )-2+cos2B=0,
)-2+cos2B=0,即2sinB·[1-cos2(
 +
+ )]-2+cos2B=0,
)]-2+cos2B=0,即2sinB+2sin2B-2+1-2sin2B=0,解得sinB=
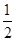 .
.由于0<B<π,所以B=
 或B=
或B=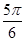 .
.(2)当B=
 时,sinA+cosC=sinA+cos(
时,sinA+cosC=sinA+cos(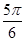 -A)=sinA-
-A)=sinA-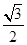 cosA+
cosA+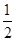 sinA=
sinA=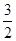 sinA-
sinA-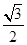 cosA=
cosA=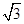 ×(
×(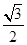 sinA-
sinA-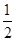 cosA)=
cosA)=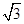 sin(A-
sin(A- ).
).由于0<A<
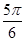 ,所以-
,所以- <A-
<A- <
<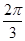 ,
,所以-
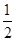 <sin(A-
<sin(A- )≤1,
)≤1,所以sinA+cosC的取值范围是(-
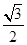 ,
,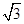 ];
];当B=
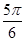 时,sinA+cosC=sinA+cos(
时,sinA+cosC=sinA+cos( -A)=sinA+
-A)=sinA+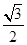 cosA+
cosA+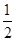 sinA=
sinA=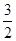 sinA+
sinA+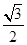 cosA=
cosA=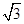 ×(
×(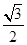 sinA+
sinA+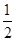 cosA)=
cosA)=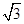 sin(A+
sin(A+ ),
),由于0<A<
 ,故
,故 <A+
<A+ <
<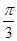 ,
,故
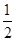 <sin(A+
<sin(A+ )<
)<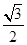 ,
,所以sinA+cosC的取值范围是(
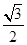 ,
,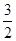 ).
).
练习册系列答案
相关题目
 其中
其中
 在
在 中,
中, 分别是角的对边,且
分别是角的对边,且 .
. ,
, ,求
,求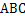 的墙面前的点
的墙面前的点 处进行射击训练.已知点
处进行射击训练.已知点 ,某目标点
,某目标点 沿墙面的射击线
沿墙面的射击线 移动,此人为了准确瞄准目标点
移动,此人为了准确瞄准目标点 的大小.若
的大小.若 则
则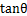 的最大值
的最大值 
 ,BD=
,BD= ,周长为18,则这个平行四边形的面积为( )
,周长为18,则这个平行四边形的面积为( )
 两地相距
两地相距 ,且
,且 地在
地在 地的正东方。一人在
地的正东方。一人在 在正北方,建筑
在正北方,建筑 在北偏西
在北偏西 ;在
;在 ,建筑
,建筑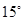 ,则两建筑
,则两建筑



 ,求C.
,求C.  中,角
中,角 所对的边分别是
所对的边分别是 ,若角
,若角 则
则 等于( ).
等于( ).


