题目内容
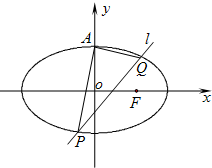 如图,已知椭圆C:
如图,已知椭圆C:| x2 |
| a2 |
| ||
| 3 |
| AP |
| AQ |
(Ⅰ)求椭圆C的方程;
(Ⅱ)求证:直线l过定点,并求出该定点N的坐标.
分析:(Ⅰ)由椭圆的解析式得到b=1,再利用椭圆的性质a2+b2=c2列出关系式,与e=
=
联立组成方程组,求出方程组的解得到a与c的值,即可确定出椭圆的解析式;
(Ⅱ)由
•
=0,利用平面斜率数量积为0时两向量垂直得到AP与AQ垂直,可得出AP与坐标轴不垂直,由A的坐标设出直线AP的方程为y=kx+1,根据两直线垂直时斜率的乘积为-1表示出直线AQ的方程,将y=kx+1代入椭圆方程,消去y得到关于x的一元二次方程,求出方程的解得到x的值,表示出P的坐标,将直线AQ方程代入椭圆方程,同理表示出Q的坐标,由P与Q的坐标,表示出直线l的两点式方程,整理后可得出直线l恒过定点N(0,-
).
| c |
| a |
| ||
| 3 |
(Ⅱ)由
| AP |
| AQ |
| 1 |
| 2 |
解答:解(Ⅰ)依题意有:e=
=
①,a2-c2=b2=1②,
联立①②解得:a=
,c=
,
则椭圆C的方程为
+y2=1;
(Ⅱ)证明:由
•
=0,得到AP⊥AQ,从而直线AP与坐标轴不垂直,
由A(0,1)可设直线AP的方程为y=kx+1,得到直线AQ的方程为y=-
x+1(k≠0),
将y=kx+1代入椭圆C的方程
+y2=1中,并整理得:(1+3k2)x2+6kx=0,
解得:x=0或x=-
,
∴P的坐标为(-
,-
+1),即(-
,
),
将上式中的k换成-
,同理可得Q(
,
),
∴直线l的方程为y=
(x-
)+
,
整理得:直线l的方程为y=
x-
,
则直线l过定点N(0,-
).
| c |
| a |
| ||
| 3 |
联立①②解得:a=
| 3 |
| 2 |
则椭圆C的方程为
| x2 |
| 3 |
(Ⅱ)证明:由
| AP |
| AQ |
由A(0,1)可设直线AP的方程为y=kx+1,得到直线AQ的方程为y=-
| 1 |
| k |
将y=kx+1代入椭圆C的方程
| x2 |
| 3 |
解得:x=0或x=-
| 6k |
| 1+3k2 |
∴P的坐标为(-
| 6k |
| 1+3k2 |
| 6k2 |
| 1+3k2 |
| 6k |
| 1+3k2 |
| 1-3k2 |
| 1+3k2 |
将上式中的k换成-
| 1 |
| k |
| 6k |
| k2+3 |
| k2-3 |
| k2+3 |
∴直线l的方程为y=
| ||||
|
| 6k |
| k2+3 |
| k2-3 |
| k2+3 |
整理得:直线l的方程为y=
| k2-1 |
| 4k |
| 1 |
| 2 |
则直线l过定点N(0,-
| 1 |
| 2 |
点评:此题考查了恒过定点的方程,以及椭圆的标准方程,涉及的知识有:椭圆的基本性质,平面向量的数量积运算,以及直线的两点式方程,其计算性较大,是一道综合性较强的试题.

练习册系列答案
相关题目
 如图,已知椭圆C:
如图,已知椭圆C: 如图,已知椭圆C:
如图,已知椭圆C: 如图,已知椭圆C:
如图,已知椭圆C: (2012•深圳一模)如图,已知椭圆C:
(2012•深圳一模)如图,已知椭圆C: 如图,已知椭圆
如图,已知椭圆