Question

【题目】若函数 在某区间[a，b]上的值域为[ta，tb]，则t的取值范围 ．

Answer 1

【答案】（ ， ）
【解析】解：函数 在（0，+∞）为增函数，某区间[a，b]上的值域为[ta，tb]，可得 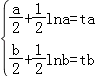，即 ，变形为 在（0，+∞）上有2个不等实数根，
故函数y= 的图象与函数y=（t﹣ ）x的图象在（0，+∞）上有两个不同的交点，
∴t﹣ ＞0，解得：t
令F（x）= ﹣tx
则F′（x）=
令F′（x）=0，解得：x=
故当x= 是函数y= 的图象与函数y=（t﹣ ）x的图象切点．
故得 ，
解得：t=
故得t的取值范围是 ．
所以答案是：（ ， ）
【考点精析】利用函数单调性的性质对题目进行判断即可得到答案，需要熟知函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集．