题目内容
设二次函数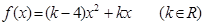 ,对任意实数
,对任意实数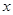 ,
,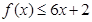 恒成立;正数数列
恒成立;正数数列 满足
满足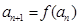 .
.
(1)求函数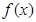 的解析式和值域;
的解析式和值域;
(2)试写出一个区间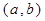 ,使得当
,使得当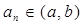 时,数列
时,数列 在这个区间上是递增数列,并说明理由;
在这个区间上是递增数列,并说明理由;
(3)若已知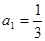 ,求证:数列
,求证:数列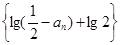 是等比数列
是等比数列
解:(1)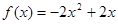 其值域为
其值域为 .…………4分
.…………4分
(2)解:当 时,数列
时,数列 在这个区间上是递增数列,证明如下:
在这个区间上是递增数列,证明如下:
设 ,则
,则 ,所以对一切
,所以对一切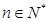 ,均有
,均有 ;………6分
;………6分
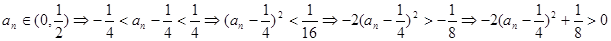 ,
,
从而得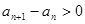 ,即
,即 ,所以数列
,所以数列 在区间
在区间 上是递增数列.………8分
上是递增数列.………8分
注:本题的区间也可以是 、
、 、
、 等无穷多个.
等无穷多个.
另解:若数列 在某个区间上是递增数列,则
在某个区间上是递增数列,则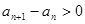
即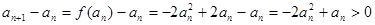
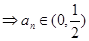 ……6分
……6分
又当 时,
时,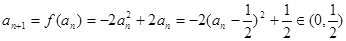 ,所以对一切
,所以对一切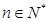 ,均有
,均有 且
且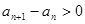 ,所以数列
,所以数列 在区间
在区间 上是递增数列.
上是递增数列.
(3)证明略
解析

练习册系列答案
相关题目
设 ,且
,且 ,则 ( )
,则 ( )
A. | B. | C. | D. |
若不等式 的解集为空集,则实数
的解集为空集,则实数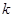 的取值范围是( )
的取值范围是( )
A.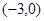 | B.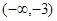 | C.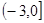 | D.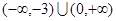 |
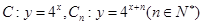 ,从
,从 上的点
上的点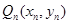 作
作 轴的垂线,交
轴的垂线,交 于点
于点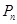 ,再从点
,再从点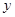 轴的垂线,交
轴的垂线,交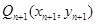 ,
,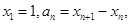
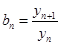 .。
.。 求数列
求数列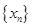 的通项公式;
的通项公式;  记
记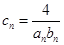 ,数列
,数列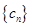 的前
的前 项和为
项和为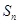 ,试比较
,试比较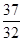 的大小
的大小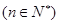 ;
;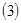 记
记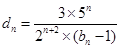 ,数列
,数列 的前
的前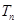 ,试证明:
,试证明: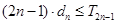 。
。 满足
满足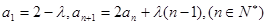
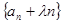 为等比数列;
为等比数列; 以及前n项和
以及前n项和 ;
; 都有
都有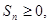 求
求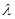 的取值范围。
的取值范围。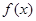 定义在区间
定义在区间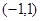 上,
上,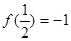 ,且当
,且当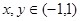 时,
时,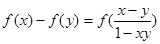 .又数列
.又数列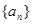 满足
满足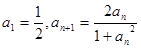 .
. 的表达式;
的表达式;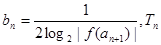 为数列
为数列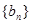 的前
的前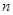 项和,若
项和,若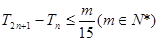 对
对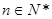 恒成立,求
恒成立,求 的最小值.
的最小值.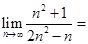 ___________.
___________. 且方向向量为
且方向向量为 的直线交椭圆
的直线交椭圆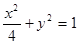 于
于 两点,记原点为
两点,记原点为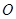 ,
,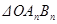 面积为
面积为 ,则
,则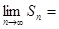 _______
_______