题目内容
求圆心在抛物线x2=4y上,且与直线x+2y+1=0相切的面积最小的圆
的方程.
的方程.
(x+1)2+ =
=
 =
=
设圆心坐标为 ,半径为r.
,半径为r.
根据已知得r= =
= (t2+2t+2)=
(t2+2t+2)= [(t+1)2+1]≥
[(t+1)2+1]≥ ,当t=-1时取等号,此时r最小为
,当t=-1时取等号,此时r最小为 ,圆心坐标为(-1,
,圆心坐标为(-1, ),故所求的圆的方程是(x+1)2+
),故所求的圆的方程是(x+1)2+ =
= .
.
 ,半径为r.
,半径为r.根据已知得r=
 =
= (t2+2t+2)=
(t2+2t+2)= [(t+1)2+1]≥
[(t+1)2+1]≥ ,当t=-1时取等号,此时r最小为
,当t=-1时取等号,此时r最小为 ,圆心坐标为(-1,
,圆心坐标为(-1, ),故所求的圆的方程是(x+1)2+
),故所求的圆的方程是(x+1)2+ =
= .
.
练习册系列答案
相关题目
 的圆心在直线
的圆心在直线 上,且与
上,且与 轴交于两点
轴交于两点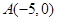 ,
, .
.
 的圆
的圆 ,点
,点 在圆
在圆 ,
, 为一组邻边的平行四边形的另一个顶点
为一组邻边的平行四边形的另一个顶点 轨迹方程.
轨迹方程.

 是圆
是圆 上任意一点,
上任意一点, 的对称点在圆上,则实数
的对称点在圆上,则实数 等于( )
等于( )


