题目内容
【题目】设函数![]() .
.
(1)当![]() 时,解方程
时,解方程![]() ;
;
(2)当![]() 时,若不等式
时,若不等式![]() 在
在![]() 上恒成立,求实数a的取值范围;
上恒成立,求实数a的取值范围;
(3)若a为常数,且函数![]() 在区间
在区间![]() 上存在零点,求实数b的取值范围.
上存在零点,求实数b的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】试题分析:(1)当![]() 时,原方程化为
时,原方程化为![]() ,先解得
,先解得![]() 即可得结果;(2)不等式
即可得结果;(2)不等式![]() 在
在![]() 上恒成立,等价于
上恒成立,等价于![]() 在
在![]() 上恒成立,求出函数
上恒成立,求出函数![]() 的最大值即可得结果;(3)函数
的最大值即可得结果;(3)函数![]() 在
在![]() 上存在零点,即方程
上存在零点,即方程![]() 在
在![]() 上有解,分类求出
上有解,分类求出![]() 的值域即可得结果.
的值域即可得结果.
试题解析:(1)当![]() 时,
时, ![]() ,所以方程即为:
,所以方程即为: ![]()
解得: ![]() 或
或![]() (舍),所以
(舍),所以![]() ;
;
(2)当![]() 时,若不等式
时,若不等式![]() 在
在![]() 上恒成立;
上恒成立;
当![]() 时,不等式恒成立,则
时,不等式恒成立,则![]() ;
;
当![]() 时,
时, ![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立,
上恒成立,
因为![]() 在
在![]() 上单调增,
上单调增, ![]() ,
, ![]() ,则
,则![]() ,
,
得![]() ;则实数
;则实数![]() 的取值范围为
的取值范围为![]() ;
;
(3)函数![]() 在
在![]() 上存在零点,即方程
上存在零点,即方程![]() 在
在![]() 上有解;
上有解;
设![]()
当![]() 时,则
时,则![]() ,且
,且![]() 在
在![]() 上单调增,
上单调增,
所以![]() ,
, ![]() ,
,
则当![]() 时,原方程有解,
时,原方程有解,
则![]() ;
;
当![]() 时,
时, ![]() ,
,
![]() 在
在![]() 上单调增,在
上单调增,在![]() 上单调减,在
上单调减,在![]() 上单调增;
上单调增;
当![]() ,即
,即![]() 时,
时, ![]() ,
,
则当![]() 时,原方程有解,则
时,原方程有解,则![]() ;
;
当![]() ,即
,即![]() 时,
时, ![]() ,
,
则当![]() 时,原方程有解,则
时,原方程有解,则![]() ;
;
当![]() 时,
时, 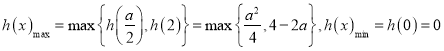 ,
,
当![]() ,即则
,即则![]() 时,
时, ![]() ,
,
则当![]() 时,原方程有解,则
时,原方程有解,则![]() ;
;
当![]() ,即则
,即则![]() 时,
时, ![]() ,
,
则当![]() 时,原方程有解,则
时,原方程有解,则![]() ;
;
综上,当![]() 时,实数
时,实数![]() 的取值范围为
的取值范围为![]() ;
;
当![]() 时,实数
时,实数![]() 的取值范围为
的取值范围为![]() ;
;
当![]() 时,实数
时,实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
相关题目
【题目】某市一家庭今年一月份、二月份和三月份煤气用量和支付费用如下表所示:
月份 | 用气量(立方米) | 煤气费(元) |
1 | 4 | 4.00 |
2 | 25 | 14.00 |
3 | 35 | 19.00 |
该市煤气收费的方法是:煤气费=基本费+超额费+保险费.
若每月用气量不超过最低额度A(A>4)立方米时,只付基本费3元和每户每月定额保险费C(0<C≤5)元;若用气量超过A立方米时,超过部分每立方米付B元.
(1)根据上面的表格求A,B,C的值;
(2)记该家庭第四月份用气为x立方米,求应交的煤气费y元.



