题目内容
已知函数f(x)= ,x∈[-1,1],函数g(x)=[f(x)]2-2af(x)+3的最小值为h(a).
,x∈[-1,1],函数g(x)=[f(x)]2-2af(x)+3的最小值为h(a).
(1)求h(a);
(2)是否存在实数m、n同时满足下列条件:
①m>n>3;
②当h(a)的定义域为[n,m]时,值域为[n2,m2]?若存在,求出m、n的值;若不存在,说明理由.
 ,x∈[-1,1],函数g(x)=[f(x)]2-2af(x)+3的最小值为h(a).
,x∈[-1,1],函数g(x)=[f(x)]2-2af(x)+3的最小值为h(a).(1)求h(a);
(2)是否存在实数m、n同时满足下列条件:
①m>n>3;
②当h(a)的定义域为[n,m]时,值域为[n2,m2]?若存在,求出m、n的值;若不存在,说明理由.
(1)h(a)= (2)不存在
(2)不存在
 (2)不存在
(2)不存在(1)∵x∈[-1,1],∴f(x)= ∈
∈ .设t=
.设t= ,t∈
,t∈ ,
,
则y=φ(t)=t2-2at+3=(t-a)2+3-a2.
当a< 时,ymin=h(a)=φ
时,ymin=h(a)=φ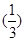 =
= ;
;
当 ≤a≤3时,ymin=h(a)=φ(a)=3-a2;
≤a≤3时,ymin=h(a)=φ(a)=3-a2;
当a>3时,ymin=h(a)=φ(3)=12-6a.
∴h(a)=
(2)假设满足题意的m、n存在,∵m>n>3,∴h(a)=12-6a在(3,+∞)上是减函数.∵h(a)的定义域为[n,m],值域为[n2,m2],∴ ,由②-①得6(m-n)=(m-n)(m+n),∵m>n>3,∴m+n=6,但这与“m>n>3”矛盾,∴满足题意的m、n不存在.
,由②-①得6(m-n)=(m-n)(m+n),∵m>n>3,∴m+n=6,但这与“m>n>3”矛盾,∴满足题意的m、n不存在.
 ∈
∈ .设t=
.设t= ,t∈
,t∈ ,
,则y=φ(t)=t2-2at+3=(t-a)2+3-a2.
当a<
 时,ymin=h(a)=φ
时,ymin=h(a)=φ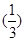 =
= ;
;当
 ≤a≤3时,ymin=h(a)=φ(a)=3-a2;
≤a≤3时,ymin=h(a)=φ(a)=3-a2;当a>3时,ymin=h(a)=φ(3)=12-6a.
∴h(a)=

(2)假设满足题意的m、n存在,∵m>n>3,∴h(a)=12-6a在(3,+∞)上是减函数.∵h(a)的定义域为[n,m],值域为[n2,m2],∴
 ,由②-①得6(m-n)=(m-n)(m+n),∵m>n>3,∴m+n=6,但这与“m>n>3”矛盾,∴满足题意的m、n不存在.
,由②-①得6(m-n)=(m-n)(m+n),∵m>n>3,∴m+n=6,但这与“m>n>3”矛盾,∴满足题意的m、n不存在.
练习册系列答案
相关题目
 是奇函数,(其中
是奇函数,(其中 )
)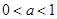 时,讨论函数f(x)的增减性;
时,讨论函数f(x)的增减性; 时,f(x)的值域是(1,
时,f(x)的值域是(1, ),求n与a的值。
),求n与a的值。 函数f(x) =max{|x+1|,|x-2|}(x∈R)的最小值是( )
函数f(x) =max{|x+1|,|x-2|}(x∈R)的最小值是( )

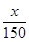 +2是否符合公司要求的奖励函数模型,并说明原因;
+2是否符合公司要求的奖励函数模型,并说明原因; 作为奖励函数模型,试确定最小的正整数a的值.
作为奖励函数模型,试确定最小的正整数a的值. 是集合M到集合N的映射, 若N="{1,2}," 则M不可能是 ( )
是集合M到集合N的映射, 若N="{1,2}," 则M不可能是 ( )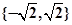


 ≤f(x1)+f(x2)成立,不等式f(x)<0的解集为A.
≤f(x1)+f(x2)成立,不等式f(x)<0的解集为A. 定义在
定义在 上,其导函数为
上,其导函数为 ,且
,且 ,当
,当 时,
时, ,则关于
,则关于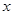 的不等式
的不等式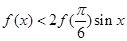 的解集为 .
的解集为 . 是定义在
是定义在 上的奇函数,则不等式
上的奇函数,则不等式 的解集为( )
的解集为( )




 满足
满足 ,且
,且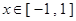 时,
时, ,则当
,则当 时,
时, 的图象的交点个数为( )
的图象的交点个数为( )