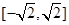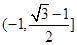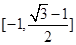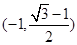题目内容
在△ ,已知
,已知
(1)求角 值;
值;
(2)求 的最大值.
的最大值.
 ,已知
,已知
(1)求角
 值;
值;(2)求
 的最大值.
的最大值.⑴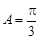 ;⑵
;⑵  .
.
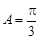 ;⑵
;⑵  .
.试题分析:⑴根据题意观察所给代数式特点可见此式中全为角的正弦,结合正弦定理可化角为边转化为
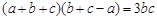 ,可将此式变形为
,可将此式变形为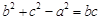 ,根据特征可联想到余弦定理
,根据特征可联想到余弦定理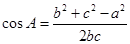 ,从而可求出
,从而可求出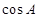 的值,即可得出
的值,即可得出 ;⑵由⑴中所求
;⑵由⑴中所求 的值,在
的值,在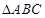 中可得
中可得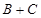 的值,这样可得
的值,这样可得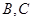 的关系,则
的关系,则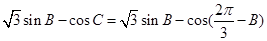 ,运用两角差的余弦公式展开可化简得
,运用两角差的余弦公式展开可化简得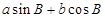 的形式,再根据公式
的形式,再根据公式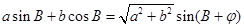 化简,最后结合函数
化简,最后结合函数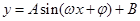 的图象,结合
的图象,结合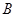 的范围,可求出
的范围,可求出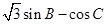 的范围,即可得到
的范围,即可得到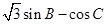 的最大值.
的最大值.试题解析:⑴因为
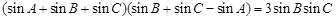 ,
,由正弦定理,得
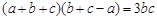 , 2分
, 2分所以
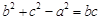 ,所以
,所以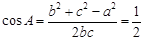 , 4分
, 4分因为
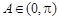 ,所以
,所以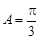 . 6分
. 6分⑵ 由
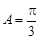 ,得
,得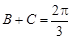 ,所以
,所以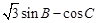
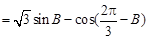
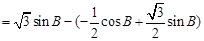
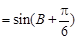 , 10分
, 10分因为
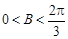 ,所以
,所以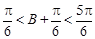 , 12分
, 12分当
 ,即
,即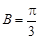 时,
时,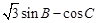 的最大值为
的最大值为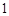 . 14分
. 14分
练习册系列答案
相关题目
 ,
, .
. 的最小正周期;
的最小正周期; 上的最大值和最小值.
上的最大值和最小值. (
( )的最小正周期为
)的最小正周期为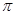 .
.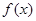 的单调增区间;
的单调增区间; 个单位,再向上平移
个单位,再向上平移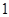 个单位,得到函数
个单位,得到函数 的图象.求
的图象.求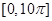 上零点的个数.
上零点的个数. 个单位,得到的图象关于直线
个单位,得到的图象关于直线 对称,则
对称,则 的最小值为
的最小值为



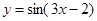 的图象,只要将函数
的图象,只要将函数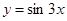 的图象( )
的图象( )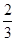 个单位
个单位 的部分图象如图所示,则函数
的部分图象如图所示,则函数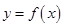 对应的解析式为( )
对应的解析式为( )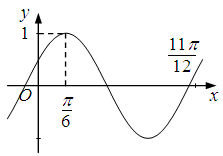



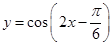
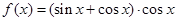 ,给出下列命题:
,给出下列命题: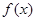 的最小正周期为
的最小正周期为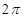 ;
;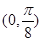 上为增函数;
上为增函数;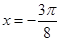 是函数
是函数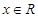 ,恒有
,恒有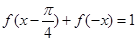 .
. ;
; ;
; ;
;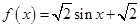 .
.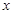 是一个三角形的最小内角,则函数
是一个三角形的最小内角,则函数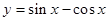 的值域是( )
的值域是( )