题目内容
已知函数f(x)=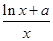 (a∈R).
(a∈R).
(1)求f(x)的极值;
(2)若函数f(x)的图象与函数g(x)=1的图象在区间(0,e2]上有公共点,求实数a的取值范围.
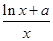 (a∈R).
(a∈R).(1)求f(x)的极值;
(2)若函数f(x)的图象与函数g(x)=1的图象在区间(0,e2]上有公共点,求实数a的取值范围.
(1)f(x)在x=e1-a处取得极大值,f(x)极大值=f(e1-a)=ea-1,无极小值
(2)[1,+∞)
(2)[1,+∞)
(1)f(x)的定义域为(0,+∞),f′(x)=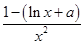 ,
,
令f′(x)=0得x=e1-a,
当x∈(0,e1-a)时,f′(x)>0,f(x)是增函数;
当x∈(e1-a,+∞)时,f′(x)<0,f(x)是减函数,
∴f(x)在x=e1-a处取得极大值,f(x)极大值=f(e1-a)=ea-1,无极小值.
(2)①当e1-a<e2时,即a>-1时,
由(1)知f (x)在(0,e1-a)上是增函数,在(e1-a,e2]上是减函数,
∴f(x)max=f(e1-a)=ea-1,
又当x=e-a时,f(x)=0,
当x∈(0,e-a]时,f(x)<0;当x∈(e-a,e2]时,f(x)>0;
∵f(x)的图象与g(x)=1的图象在(0,e2]上有公共点,
∴ea-1≥1,解得a≥1,又a>-1,所以a≥1.
②当e1-a≥e2时,即a≤-1时,f(x)在(0,e2]上是增函数,
∴f(x)在(0,e2]上的最大值为f(e2)=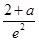 ,
,
所以原问题等价于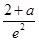 ≥1,解得a≥e2-2.
≥1,解得a≥e2-2.
又a≤-1,所以此时a无解.
综上,实数a的取值范围是[1,+∞).
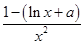 ,
,令f′(x)=0得x=e1-a,
当x∈(0,e1-a)时,f′(x)>0,f(x)是增函数;
当x∈(e1-a,+∞)时,f′(x)<0,f(x)是减函数,
∴f(x)在x=e1-a处取得极大值,f(x)极大值=f(e1-a)=ea-1,无极小值.
(2)①当e1-a<e2时,即a>-1时,
由(1)知f (x)在(0,e1-a)上是增函数,在(e1-a,e2]上是减函数,
∴f(x)max=f(e1-a)=ea-1,
又当x=e-a时,f(x)=0,
当x∈(0,e-a]时,f(x)<0;当x∈(e-a,e2]时,f(x)>0;
∵f(x)的图象与g(x)=1的图象在(0,e2]上有公共点,
∴ea-1≥1,解得a≥1,又a>-1,所以a≥1.
②当e1-a≥e2时,即a≤-1时,f(x)在(0,e2]上是增函数,
∴f(x)在(0,e2]上的最大值为f(e2)=
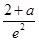 ,
,所以原问题等价于
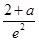 ≥1,解得a≥e2-2.
≥1,解得a≥e2-2.又a≤-1,所以此时a无解.
综上,实数a的取值范围是[1,+∞).

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 ,
, .
. 的极值;(2)若
的极值;(2)若 恒成立,求实数
恒成立,求实数 的值;
的值;
 有两个极值点
有两个极值点 、
、 (
(
 的取值范围,并证明
的取值范围,并证明 .
.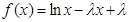 (
( ).
). 的单调区间;
的单调区间; 使
使 上恒成立?若存在,请求实数
上恒成立?若存在,请求实数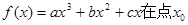 处取得极小值-4,使其导函数
处取得极小值-4,使其导函数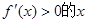 的取值范围为(1,3)。
的取值范围为(1,3)。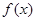 的解析式及
的解析式及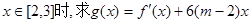 的最大值。
的最大值。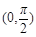 上的函数
上的函数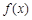 ,
,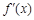 是它的导函数,且恒有
是它的导函数,且恒有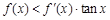 成立,则( )
成立,则( )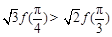
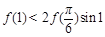
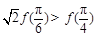
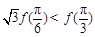
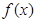 是定义在
是定义在 上的可导函数,其导函数为
上的可导函数,其导函数为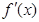 ,且有
,且有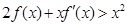 ,则不等式
,则不等式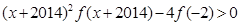 的解集为( )
的解集为( )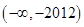
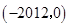

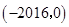
 是二次函数,方程
是二次函数,方程 有两个相等的实数根,且
有两个相等的实数根,且 。
。 把
把 在
在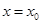 处取最大值。以下各式正确的序号为 .
处取最大值。以下各式正确的序号为 .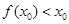 ②
②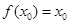 ③
③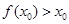 ④
④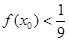 ⑤
⑤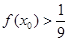
 在
在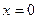 处连续,则实数
处连续,则实数 的值为_____________.
的值为_____________.