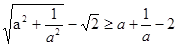题目内容
设z=kx+y,其中实数x、y满足
若z的最大值为12,则实数k=______.
|
作出不等式组
表示的平面区域,得到如图的△ABC及其内部,

其中A(2,0),B(2,3),C(4,4)
设z=F(x,y)=kx+y,将直线l:z=kx+y进行平移,可得
①当k<0时,直线l的斜率-k>0,
由图形可得当l经过点B(2,3)或C(4,4)时,z可达最大值,
此时,zmax=F(2,3)=2k+3或zmax=F(4,4)=4k+4
但由于k<0,使得2k+3<12且4k+4<12,不能使z的最大值为12,
故此种情况不符合题意;
②当k≥0时,直线l的斜率-k≤0,
由图形可得当l经过点C时,目标函数z达到最大值
此时zmax=F(4,4)=4k+4=12,解之得k=2,符合题意
综上所述,实数k的值为2
故答案为:2
|

其中A(2,0),B(2,3),C(4,4)
设z=F(x,y)=kx+y,将直线l:z=kx+y进行平移,可得
①当k<0时,直线l的斜率-k>0,
由图形可得当l经过点B(2,3)或C(4,4)时,z可达最大值,
此时,zmax=F(2,3)=2k+3或zmax=F(4,4)=4k+4
但由于k<0,使得2k+3<12且4k+4<12,不能使z的最大值为12,
故此种情况不符合题意;
②当k≥0时,直线l的斜率-k≤0,
由图形可得当l经过点C时,目标函数z达到最大值
此时zmax=F(4,4)=4k+4=12,解之得k=2,符合题意
综上所述,实数k的值为2
故答案为:2

练习册系列答案
相关题目
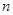 个图形中有
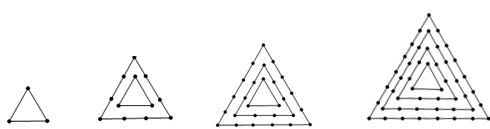
个图形中有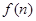 .
.
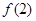 ,
,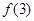 ,
,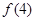 ,
, ;
;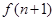 的关系,并求出
的关系,并求出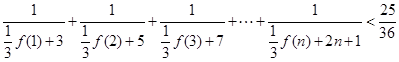 (
(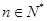 ).
).