题目内容
( 14分)已知函数 在一个周期内的部分函数图象如图所示.
在一个周期内的部分函数图象如图所示.
(1)( 6分)函数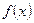 的解析式.
的解析式.
(2)( 4分)函数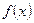 的单调递增区间.
的单调递增区间.
(3) ( 4分)函数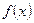 在区间
在区间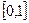 上的最大值和最小值.
上的最大值和最小值.
 在一个周期内的部分函数图象如图所示.
在一个周期内的部分函数图象如图所示.(1)( 6分)函数
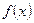 的解析式.
的解析式.(2)( 4分)函数
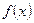 的单调递增区间.
的单调递增区间.(3) ( 4分)函数
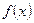 在区间
在区间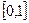 上的最大值和最小值.
上的最大值和最小值.
(1)由函数图象知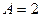 …………………………………………………………1分
…………………………………………………………1分
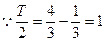
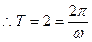 则
则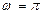 …………………………………………………………3分
…………………………………………………………3分
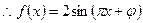
又由
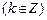 得:
得:
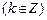 ,
,
因为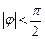 ,所以
,所以 …………………………………………………………5分
…………………………………………………………5分
故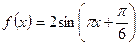 ………………………
……………………… …………………………………6分
…………………………………6分
(2)由 ,
, ………………………………………7分
………………………………………7分
得: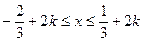 ,
, ………………………………………9分
………………………………………9分
则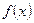 的单调递增区间为
的单调递增区间为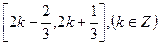 …
… …………………………10分
…………………………10分
(3)法Ⅰ: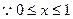
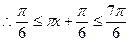 ……………………………11分
……………………………11分
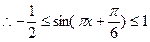
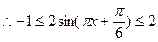 ……………………………………………13分
……………………………………………13分
故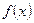 在区间
在区间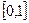 上的最大值为
上的最大值为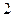 ,最小值为
,最小值为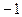 .……………………………14分
.……………………………14分
法Ⅱ:由函数的图象知:直线 是函数
是函数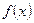 的对称轴,
的对称轴,
则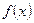 在
在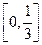 上单调递增,在
上单调递增,在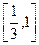 上单调递减.……………………………………11分
上单调递减.……………………………………11分
故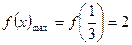

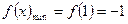 …………………………
………………………… …………13分
…………13分
即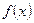 在区间
在区间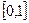 上的最大值为
上的最大值为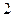 ,最小值为
,最小值为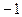 .………………………………………14分
.………………………………………14分
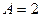 …………………………………………………………1分
…………………………………………………………1分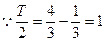
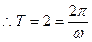 则
则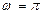 …………………………………………………………3分
…………………………………………………………3分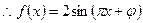
又由

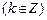 得:
得:
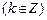 ,
,因为
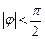 ,所以
,所以 …………………………………………………………5分
…………………………………………………………5分故
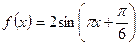 ………………………
……………………… …………………………………6分
…………………………………6分(2)由
 ,
, ………………………………………7分
………………………………………7分得:
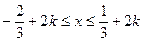 ,
, ………………………………………9分
………………………………………9分则
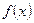 的单调递增区间为
的单调递增区间为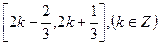 …
… …………………………10分
…………………………10分(3)法Ⅰ:
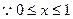
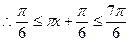 ……………………………11分
……………………………11分 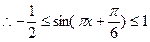
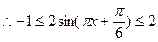 ……………………………………………13分
……………………………………………13分 故
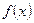 在区间
在区间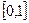 上的最大值为
上的最大值为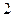 ,最小值为
,最小值为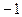 .……………………………14分
.……………………………14分法Ⅱ:由函数的图象知:直线
 是函数
是函数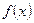 的对称轴,
的对称轴,则
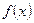 在
在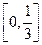 上单调递增,在
上单调递增,在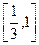 上单调递减.……………………………………11分
上单调递减.……………………………………11分故
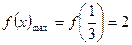

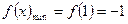 …………………………
………………………… …………13分
…………13分即
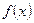 在区间
在区间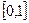 上的最大值为
上的最大值为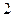 ,最小值为
,最小值为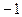 .………………………………………14分
.………………………………………14分略

练习册系列答案
相关题目
 的图象上所有的点向右平移
的图象上所有的点向右平移 个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是
个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是



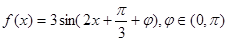 满足
满足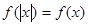 ,则
,则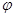 的值为( )
的值为( )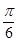
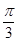
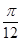
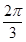
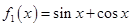 ,
,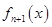 是
是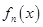 的导函数,即
的导函数,即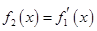 ,
,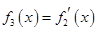 ,…,
,…,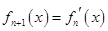 ,
,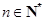 ,则
,则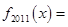 ( )
( )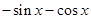
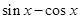
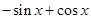
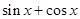
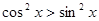 的解集为( )
的解集为( )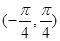
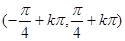
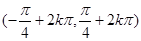
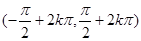 以上
以上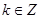
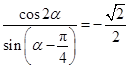 ,则
,则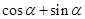 的值为( )
的值为( )
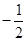


 ABC中,
ABC中,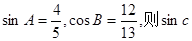 的值为( )
的值为( )

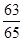
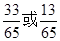
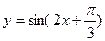 先向右平移
先向右平移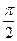 个单位,然后向下平移2个单位后所得的
个单位,然后向下平移2个单位后所得的