题目内容
不等式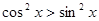 的解集为( )
的解集为( )
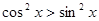 的解集为( )
的解集为( )A.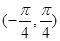 | B.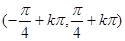 |
C.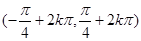 | D.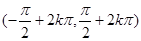 以上 以上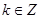 |
B
分析:先将sin2x<cos2x化为cos2x-sin2x>0,就是cos2x>0,然后求解不等式即可得到x的取值范围.
解:∵sin2x<cos2x,
∴cos2x-sin2x>0,
由二倍角公式可得,cos2x>0
∴2kπ- π<2x<2kπ+
π<2x<2kπ+ π,k∈Z
π,k∈Z
解得:kπ-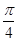 <x<kπ+
<x<kπ+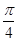
所以x的取值范围是{x|kπ-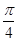 <x<kπ+
<x<kπ+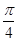 ,k∈Z}
,k∈Z}
故选B
解:∵sin2x<cos2x,
∴cos2x-sin2x>0,
由二倍角公式可得,cos2x>0
∴2kπ-
 π<2x<2kπ+
π<2x<2kπ+ π,k∈Z
π,k∈Z解得:kπ-
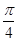 <x<kπ+
<x<kπ+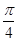
所以x的取值范围是{x|kπ-
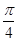 <x<kπ+
<x<kπ+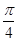 ,k∈Z}
,k∈Z}故选B

练习册系列答案
相关题目
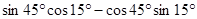 的值为 ( )
的值为 ( )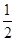
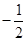
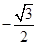

 ,
, ,
, ,则( )
,则( )



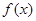 =
=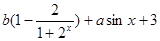 (
(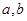 为常数),若f(x)在(0,+∞)上有最大值10,则
为常数),若f(x)在(0,+∞)上有最大值10,则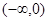 上有( )
上有( ) ,则下列等式对
,则下列等式对 恒成立的是( )
恒成立的是( )



 在一个周期内的部分函数图象如图所示.
在一个周期内的部分函数图象如图所示.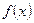 的解析式.
的解析式. 上的最大值和最小值.
上的最大值和最小值.
 B.
B. C.
C. D.
D.
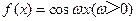 ,将
,将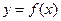 的图像向右平移
的图像向右平移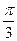 个单位长度后,所得的图像与原图像重合,则
个单位长度后,所得的图像与原图像重合,则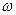 的最小值等于
的最小值等于 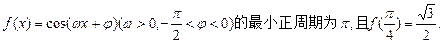
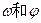 的值;
的值;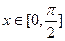 ,求
,求 的取值范围.
的取值范围.