题目内容
已知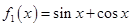 ,
,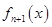 是
是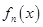 的导函数,即
的导函数,即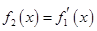 ,
,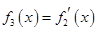 ,…,
,…,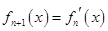 ,
,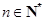 ,则
,则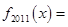 ( )
( )
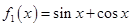 ,
,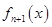 是
是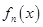 的导函数,即
的导函数,即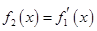 ,
,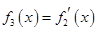 ,…,
,…,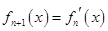 ,
,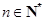 ,则
,则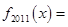 ( )
( )A.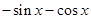 | B.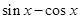 | C.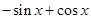 | D.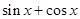 |
A
专题:计算题;综合题.
分析:先求出f2(x)、f3(x)、f4(x),观察所求的结果,归纳其中的周期性规律,求解即可.
解答:解:f2(x)=f1′(x)=cosx-sinx,
f3(x)=(cosx-sinx)′=-sinx-cosx,
f4(x)=-cosx+sinx,f5(x)=sinx+cosx,
以此类推,可得出fn(x)=fn+4(x)
f2011(x)=f3(x)=-sinx-cosx,
故选A.
点评:此题是中档题.本题考查三角函数的导数、周期性、及观察归纳思想的运用.

练习册系列答案
相关题目
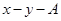 (A为常数)则
(A为常数)则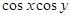 的最大值是 ( )
的最大值是 ( )




 个单位长度
个单位长度 个单位长度
个单位长度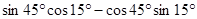 的值为 ( )
的值为 ( )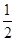
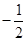
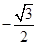

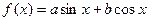 的图象经过点
的图象经过点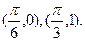
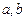 的值;
的值;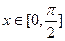 ,求函数
,求函数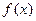 的最大值及此时
的最大值及此时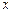 的值.
的值. ,
, ,
, ,则( )
,则( )



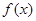 =
=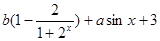 (
(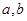 为常数),若f(x)在(0,+∞)上有最大值10,则
为常数),若f(x)在(0,+∞)上有最大值10,则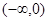 上有( )
上有( ) 在一个周期内的部分函数图象如图所示.
在一个周期内的部分函数图象如图所示.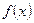 的解析式.
的解析式.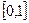 上的最大值和最小值.
上的最大值和最小值.
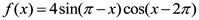 已知函数
已知函数  ,
,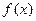 的最小正周期;
的最小正周期; 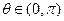 ,
,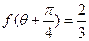 , 求
, 求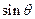 的值.
的值.