Question

2．已知菱形ABCD的边长为2，∠BAD=60°，现沿BD将△ABD折起并使得AC=$\sqrt{3}$（如图所示），则二面角A-BD-C的大小为（　　）

• A． 30°
• B． 60°
• C． 90°
• D． 120°

Answer 1

分析 根据二面角的平面角的定义先找出二面角的平面角，然后结合三角形的边角关系进行求解即可．

解答 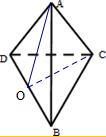解：取BD的中点O，
连接AO，OC，
∵菱形ABCD的边长为2，∠BAD=60°，
∴△ABD，△BCD为正三角形，
则AO⊥BD，OC⊥BD，
即∠AOC是二面角A-BD-C的平面角，
∵菱形ABCD是边长为2，
∴AO=OC=$\sqrt{3}$，
∵AC=$\sqrt{3}$，
∴△AOC为正三角形，
则∠AOC=60°，
故选：B

点评 本题主要考查二面角的求解，根据二面角平面角的定义，先找出平面角是解决本题的关键．