题目内容
【题目】如图1,在梯形ABCD中,AB//CD,AB=3,CD=6,过A,B分别作CD的垂线,垂足分别为E,F,已知DE=1,AE=3,将梯形ABCD沿AE,BF同侧折起,使得平面ADE⊥平面ABFE,平面ADE∥平面BCF,得到图2.
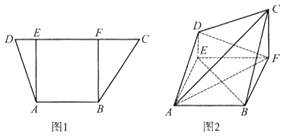
(1)证明:BE//平面ACD;
(2)求三棱锥C﹣AED的体积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)设AF∩BE=O,取AC中点M,连接OM,证明四边形DEOM为平行四边形,从而得到DM//OE,再利用线面平行判定定理证得结论;
(2)由点C到平面ADE的距离等于点F到平面ADE的距离,即可得到![]()
将数据代入即可得答案.
(1)证明:设AF∩BE=O,取AC中点M,连接OM.
∵四边形ABFE为正方形,∴O为AF中点,
∵M为AC中点,∴![]() ,
,![]() .
.
∵平面ADE![]() 平面ABFE,平面ADE
平面ABFE,平面ADE![]() 平面ABFE
平面ABFE![]() AE,DE
AE,DE![]() AE,DE
AE,DE![]() 平面ADE,
平面ADE,
∴DE![]() 平面ABFE;
平面ABFE;
又∵平面ADE//平面BCF,∴平面BCF⊥平面ABFE,同理,CF⊥平面ABFE.
又∵DE=1,FC=2,∴![]() 且
且![]() ,
,
∴![]() ,且OM
,且OM![]() DE,∴四边形DEOM为平行四边形,∴DM//OE.
DE,∴四边形DEOM为平行四边形,∴DM//OE.
∵DM平面ADC,BE平面ADC,∴BE//平面ADC.
(2)∵CF![]() DE,DE
DE,DE![]() 平面ADE,CF
平面ADE,CF![]() 平面ADE,
平面ADE,
∴CF![]() 平面ADE,
平面ADE,
∴点C到平面ADE的距离等于点F到平面ADE的距离.
∴![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目