题目内容
已知三棱锥A-BCD的外接球球心在CD上,且AB=BC=
,BD=1,在外接球面上两点A、B间的球面距离是( )
| 3 |
分析:先求出球的半径,然后求出∠AOB的余弦值,求出球心角,再求其外接球面上两点A,B间的球面距离.
解答:解:由球心在CD上,得CD是球的直径,
∴∠CBD=90°,∵BC=
,BD=1,
∴CD=2,得球的半径R=1,OA=OB=1
在三角形OAB中,由余弦定理得:
COS∠AOB=
=-
,⇒∠AOB=
.
∴l=Rθ=
.
∴两点A、B间的球面距离是
.
故选C.
∴∠CBD=90°,∵BC=
| 3 |
∴CD=2,得球的半径R=1,OA=OB=1
在三角形OAB中,由余弦定理得:
COS∠AOB=
12+12-(
| ||
| 2×1×1 |
| 1 |
| 2 |
| 2π |
| 3 |
∴l=Rθ=
| 2π |
| 3 |
∴两点A、B间的球面距离是
| 2π |
| 3 |
故选C.
点评:本题主要考查了球内接多面体、余弦定理的应用、球面距离及相关计算等.考查了学生观察分析和基本的运算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
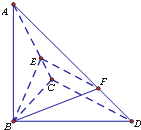 已知三棱锥A-BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是直线AC,AD上的点,且
已知三棱锥A-BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是直线AC,AD上的点,且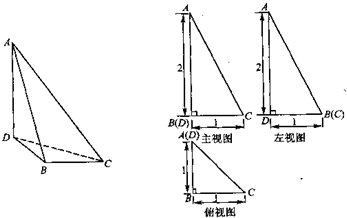 (2009•大连一模)已知三棱锥A-BCD及其三视图如图所示.
(2009•大连一模)已知三棱锥A-BCD及其三视图如图所示.