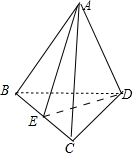
题目内容

已知三棱锥A-BCD的各棱长均为1，且E是BC的中点，则
AE
•
CD
=（　　）
分析：先求出DE的长，再根据向量的三角形法则把
AE
•
CD
转化为
DA
•
DC
-
DE
•
DC
；再结合数量积计算公式即可得到结论．
解答：解：在△BDC中，得DE=
3
2

∵
AE
•
CD
=(
AD
+
DE
)•
CD
=
AD
•
CD
+
DE
•
CD
=
DA
•
DC
-
DE
•
DC

=|
DA
|•|
DC
|cos∠ADC-|
DE
|•|
DC
|cos∠EDC
=1×1×
1
2
-1×
3
2
×
3
2

=-
1
4
．
故选D．
点评：本题主要考查数量积的应用以及向量的三角形法则．在解决向量问题直接不好找时，一般是根据三角形法则或平行四边形法则把所求问题转化．
练习册系列答案
相关题目
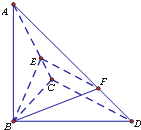已知三棱锥A-BCD中，∠BCD=90°，BC=CD=1，AB⊥平面BCD，∠ADB=60°，E，F分别是直线AC，AD上的点，且
AE
AC
=
AF
AD
=λ．
（1）求二面角B-CD-A平面角的余弦值
（2）当λ为何值时，平面BEF⊥平面ACD．
已知三棱锥A-BCD中，AB=CD，且直线AB与CD成60°角，点M、N分别是BC、AD的中点，则直线AB和MN所成的角是
60°
60°
．
（1992•云南）已知三棱锥A-BCD的体积是V，棱BC的长是a，面ABC和面DBC的面积分别是S1和S2．设面ABC和面DBC所成的二面角是α，那么sinα=
3aV
2S1S2
3aV
2S1S2
．
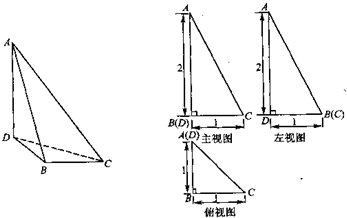（2009•大连一模）已知三棱锥A-BCD及其三视图如图所示．
（I）若DE⊥AB于E，DE⊥AC于F，求证：AC⊥平面DEF；
（Ⅱ）求二面角B-AC-D的大小．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网