题目内容
（1992•云南）已知三棱锥A-BCD的体积是V，棱BC的长是a，面ABC和面DBC的面积分别是S1和S2．设面ABC和面DBC所成的二面角是α，那么sinα=
．
| 3aV |
| 2S1S2 |
| 3aV |
| 2S1S2 |
分析：作出三棱锥A-BCD，过顶点A向底面BCD作AH⊥平面BCD，在平面ABC内作AE⊥BC，连结HE，从而得到二面角
A-BC-D的平面角，把三棱锥的高AH用体积和底面积表示，把斜高用△ABC的面积和边BC的长度表示，在直角三角形AHE中可求角α的正弦值．
A-BC-D的平面角，把三棱锥的高AH用体积和底面积表示，把斜高用△ABC的面积和边BC的长度表示，在直角三角形AHE中可求角α的正弦值．
解答：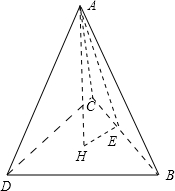
解：如图，过顶点A向底面BCD作AH⊥平面BCD，
在平面ABC内作AE⊥BC，连结HE，
根据三垂线定理可知，HE⊥BC，
所以∠AEH是二面角A-BC-D的平面角，则∠AEH=α，
由已知S△BCD=S2，三棱锥A-BCD的体积为V=
S2•AH，AH=
，
S△ABC=S1=
AE•BC，AE=2
，
sinα=
=
=
．
所以面ABC和面DBC所成二面角的正弦值为
．
故答案为
．
解：如图，过顶点A向底面BCD作AH⊥平面BCD，在平面ABC内作AE⊥BC，连结HE，
根据三垂线定理可知，HE⊥BC，
所以∠AEH是二面角A-BC-D的平面角，则∠AEH=α，
由已知S△BCD=S2，三棱锥A-BCD的体积为V=
| 1 |
| 3 |
| 3V |
| S2 |
S△ABC=S1=
| 1 |
| 2 |
| S1 |
| a |
sinα=
| AH |
| AE |
| ||
|
| 3aV |
| 2S1S2 |
所以面ABC和面DBC所成二面角的正弦值为
| 3aV |
| 2S1S2 |
故答案为
| 3aV |
| 2S1S2 |
点评：本题考查了二面角的平面角的求法，考查了锥体的体积公式，考查了学生的空间想象能力和思维能力，是中档题．
练习册系列答案
口算题卡加应用题集训系列答案
相关题目