题目内容
已知三棱锥A-BCD中,AB=CD,且直线AB与CD成60°角,点M、N分别是BC、AD的中点,则直线AB和MN所成的角是
60°
60°
.分析:取BD中点为O,连接MN、NO、MO.根据题中条件可知:NO=MO,且∠MON=60°,即△MON为等边三角形.由∠MNO=60°,AB∥NO,推导出AB和MN所成的角为60°.
解答:解:取BD中点为O,连接MN、NO、MO.
∵AB=CD,OM
CD,ON
AB,直线AB与CD成60°角,
∴NO=MO,且∠MON=60°,即△MON为等边三角形.
所以∠MNO=60°,
因为AB∥NO,所以AB和MN所成的角为60°.
故答案为:60°.
∵AB=CD,OM
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
| 1 |
| 2 |
∴NO=MO,且∠MON=60°,即△MON为等边三角形.
所以∠MNO=60°,
因为AB∥NO,所以AB和MN所成的角为60°.
故答案为:60°.
点评:本题考查异面直线所成的角的求法,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
相关题目
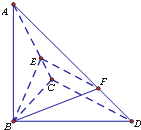 已知三棱锥A-BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是直线AC,AD上的点,且
已知三棱锥A-BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是直线AC,AD上的点,且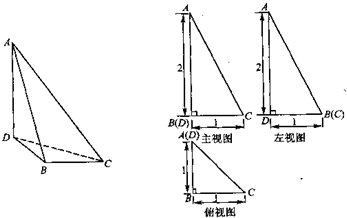 (2009•大连一模)已知三棱锥A-BCD及其三视图如图所示.
(2009•大连一模)已知三棱锥A-BCD及其三视图如图所示.