题目内容
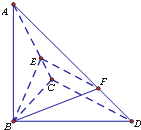已知三棱锥A-BCD中，∠BCD=90°，BC=CD=1，AB⊥平面BCD，∠ADB=60°，E，F分别是直线AC，AD上的点，且| AE |
| AC |
| AF |
| AD |
（1）求二面角B-CD-A平面角的余弦值
（2）当λ为何值时，平面BEF⊥平面ACD．
分析：（1）由于AB⊥平面BCD，可得AB⊥CD，及∠BCD=90°，可得CD⊥平面ABC．于是AC⊥CD．可得∠ACD是二面角B-CD-A平面角的平面角．在Rt△BCD，BC=CD=1，可得BD=
．在Rt△ABD中，∠ADB=60°．可得AB=BD•tan60°=
．利用勾股定理可得AC=
=
．进而得到cos∠ACB．
（2）由（1）可知：BC⊥平面ACB，可得CD⊥BE．因此当BE⊥AC时，可得BE⊥平面ACD，满足平面BEF⊥ACD．当BE⊥AC时，由射影定理可得AB2=AE•AC，BC2=EC•AC，得到
=
=
=6．即可得到
．
| 2 |
| 6 |
| AB2+BC2 |
| 7 |
（2）由（1）可知：BC⊥平面ACB，可得CD⊥BE．因此当BE⊥AC时，可得BE⊥平面ACD，满足平面BEF⊥ACD．当BE⊥AC时，由射影定理可得AB2=AE•AC，BC2=EC•AC，得到
| AE |
| EC |
| AB2 |
| BC2 |
(
| ||
| 12 |
| AE |
| AC |
解答：解：（1）∵AB⊥平面BCD，∴AB⊥CD，
∵∠BCD=90°，∴CD⊥BC．
又AB∩BC=B．∴CD⊥平面ABC．
∴AC⊥CD．
∴∠ACD是二面角B-CD-A平面角的平面角．
在Rt△BCD，BC=CD=1，∴BD=
．
在Rt△ABD中，∠ADB=60°．∴AB=BD•tan60°=
．
∴AC=
=
．
∴cos∠ACB=
=
=
．
（2）由（1）可知：BC⊥平面ACB，∴CD⊥BE．
因此当BE⊥AC时，可得BE⊥平面ACD，∴平面BEF⊥ACD．
当BE⊥AC时，由AB2=AE•AC，BC2=EC•AC，
∴
=
=
=6．
∴
=
．
∵∠BCD=90°，∴CD⊥BC．
又AB∩BC=B．∴CD⊥平面ABC．
∴AC⊥CD．
∴∠ACD是二面角B-CD-A平面角的平面角．
在Rt△BCD，BC=CD=1，∴BD=
| 2 |
在Rt△ABD中，∠ADB=60°．∴AB=BD•tan60°=
| 6 |
∴AC=
| AB2+BC2 |
| 7 |
∴cos∠ACB=
| BC |
| AC |
| 1 | ||
|
| ||
| 7 |
（2）由（1）可知：BC⊥平面ACB，∴CD⊥BE．
因此当BE⊥AC时，可得BE⊥平面ACD，∴平面BEF⊥ACD．
当BE⊥AC时，由AB2=AE•AC，BC2=EC•AC，
∴
| AE |
| EC |
| AB2 |
| BC2 |
(
| ||
| 12 |
∴
| AE |
| AC |
| 6 |
| 7 |
点评：本题考查了线面、面面垂直的判定与性质定理、二面角的平面角、勾股定理、射影定理、平行线分线段成比例定理等基础知识与基本方法，属于难题．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
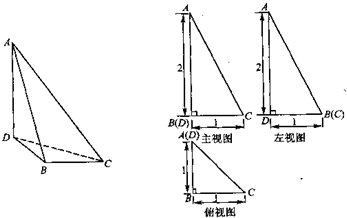（2009•大连一模）已知三棱锥A-BCD及其三视图如图所示．