题目内容
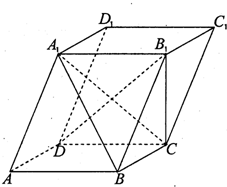 (2011•重庆三模)如题19图,平行六面体ABCD-A1B1C1D1的下底面ABCD是边长为a的正方形,AA1=
(2011•重庆三模)如题19图,平行六面体ABCD-A1B1C1D1的下底面ABCD是边长为a的正方形,AA1=| 2 |
(I)证明:B1D⊥面A1CB;
(II)求二面角A1-BC-B1的大小.
分析:(I) 由已知,点A1在下底面ABCD上的射影恰为D点,点B1在下底面ABCD上的射影恰为C点.易证BC⊥面B1DC,得出BC⊥B1D,再根据,又AA1=
a,AD=a,求出A1D=a,判断出A1B1CD为正方形,再得出 B1D⊥A1C,且BC∩A1C=C,于是B1D⊥面A1CB;
(Ⅱ)法一:在(I)的基础上,已有BC⊥面B1DC,∴BC⊥B1C,BC⊥A1C,∴∠B1CA1为二面角A1-BC-B1的 平面角,设A1C∩B1D=O,利用sin∠B1CA1=
=
,求得∠B1CA1=45°;
法二:以D点为原点,建立空间直角坐标系,分别求出平面A1BC的法向量为
,平面B1BC的法向量为
,利用<
的夹角求出二面角A1-BC-B1的大小.
| 2 |
(Ⅱ)法一:在(I)的基础上,已有BC⊥面B1DC,∴BC⊥B1C,BC⊥A1C,∴∠B1CA1为二面角A1-BC-B1的 平面角,设A1C∩B1D=O,利用sin∠B1CA1=
| B1O |
| B1C |
| ||
| 2 |
法二:以D点为原点,建立空间直角坐标系,分别求出平面A1BC的法向量为
| m |
| n |
| m, |
| n |
解答:解:(I)∵点A1在下底面ABCD上的射影恰为D点,∴点B1在下底面ABCD上的射影恰为C点.
即B1C⊥面ABCD,∴B1C⊥BC 又BC⊥CD,BC⊥面B1DC,∴BC⊥B1D,又AA1=
a,AD=a,
∴A1D=a,即A1B1CD为正方形,∴B1D⊥A1C,∴B1D⊥面A1CB.
(II)法一:BC⊥面B1DC,∴BC⊥B1C,BC⊥A1C,∴∠B1CA1为二面角A1-BC-B1的 平面角,
设A1C∩B1D=O,则B1C=A1D=a B1D=
a,∴B1O=
a,∴sin∠B1CA1=
=
,∠B1CA1=45°,
∴二面角A1-BC-B1的大小是45°.
法二:建立空间直角坐标系如图所示,

则A1(0,0,a),B1(0,a,a),B(a,a,0),C(0,a,0)
=(0,a,-a)
=(-a,0,0)
=(0,0,-a)
设平面A1BC的法向量为
=(x,y,z,)则
即
令y=1,得
=(0,1,1)
设平面B1BC的法向量为
=(x′,y′,z′),则
即
,
令y′=1,得
=(0,1,0)
cos<
>=
=
,<
>=45°,又二面角A1-BC-B1的为锐二面角,所以其大小为45°.
即B1C⊥面ABCD,∴B1C⊥BC 又BC⊥CD,BC⊥面B1DC,∴BC⊥B1D,又AA1=
| 2 |
∴A1D=a,即A1B1CD为正方形,∴B1D⊥A1C,∴B1D⊥面A1CB.
(II)法一:BC⊥面B1DC,∴BC⊥B1C,BC⊥A1C,∴∠B1CA1为二面角A1-BC-B1的 平面角,
设A1C∩B1D=O,则B1C=A1D=a B1D=
| 2 |
| ||
| 2 |
| B1O |
| B1C |
| ||
| 2 |
∴二面角A1-BC-B1的大小是45°.
法二:建立空间直角坐标系如图所示,

则A1(0,0,a),B1(0,a,a),B(a,a,0),C(0,a,0)
| A1C |
| BC |
| B1C |
设平面A1BC的法向量为
| m |
|
|
令y=1,得
| m |
设平面B1BC的法向量为
| n |
|
|
令y′=1,得
| n |
cos<
| m, |
| n |
| 1 | ||
|
| ||
| 2 |
| m, |
| n |
点评:本题考查直线和平面垂直关系,二面角求解,考查转化的思想方法(空间问题平面化)空间想象能力,计算能力.利用空间向量的知识,则使问题论证与求解演变成了代数运算,降低了思维难度,使人们解决问题更加方便.

练习册系列答案
相关题目