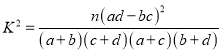Question

【题目】选修4-4：坐标系与参数方程

在直角坐标系中，已知点，曲线的参数方程为（为参数）．以原点为极点， 轴正半轴为极轴建立极坐标系，直线的极坐标方程为．

（Ⅰ）判断点与直线的位置关系并说明理由；

（Ⅱ）设直线与曲线的两个交点分别为， ，求的值．

Answer 1

【答案】(1)详见解析;(2) .

【解析】试题分析:(1)先将直线的极坐标方程化为普通方程,再代入点验证,得出结论;(2)将直线l的参数方程代入曲线C的方程,根据t的几何意义进行求解.

试题解析:（Ⅰ）点在直线上，理由如下：

直线： ，即，即，

所以直线的直角坐标方程为，易知点在直线上．

（Ⅱ）由题意，可得直线的参数方程为（为参数），曲线的普通方程为，

直线的参数方程代入曲线的普通方程，得，∴，

根为， ，∴，∴，故与异号，

∴，

∴，

∴ ．

点睛:把直角坐标系的原点作为极点,x轴的正半轴作为极轴,并在两种坐标系中取相同的单位长度单位.设M是平面内任意一点,它的直角坐标为(x,y),极坐标是,则它们的关系是： .直线的参数方程中参数t的几何意义是:t的绝对值等于直线上的动点M到定点P的距离.