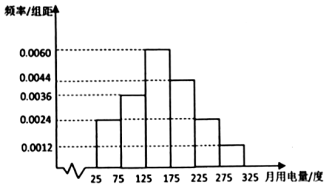
题目内容
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的部分图象如图所示,若将f(x)的图象上所有点向右平移
)的部分图象如图所示,若将f(x)的图象上所有点向右平移 ![]() 个单位得到函数g(x)的图象,则函数g(x)的单调增区间为( )
个单位得到函数g(x)的图象,则函数g(x)的单调增区间为( ) 
A.![]() ,k∈Z
,k∈Z
B.![]() ,k∈Z
,k∈Z
C.![]() ,k∈Z
,k∈Z
D.![]() ,k∈Z
,k∈Z
【答案】A
【解析】解:由图可知A=2,T=4( ![]() ﹣
﹣ ![]() )=π, ∴=
)=π, ∴= ![]() =2.
=2.
∵由图可得点( ![]() ,2)在函数图象上,可得:2sin(2×
,2)在函数图象上,可得:2sin(2× ![]() +φ)=2,解得:2×
+φ)=2,解得:2× ![]() +φ=2kπ+
+φ=2kπ+ ![]() ,k∈Z,
,k∈Z,
∴由|φ|< ![]() ,可得:φ=
,可得:φ= ![]() ,
,
∴f(x)=2sin(2x+ ![]() ).
).
∵若将y=f(x)的图象向右平移 ![]() 个单位后,得到的函数解析式为:g(x)=2sin[2(x﹣
个单位后,得到的函数解析式为:g(x)=2sin[2(x﹣ ![]() )+
)+ ![]() ]=2sin(2x+
]=2sin(2x+ ![]() ).
).
∴由2kπ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,可得kπ﹣
,k∈Z,可得kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,k∈Z,
,k∈Z,
∴函数g(x)的单调增区间为:[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ],k∈Z.
],k∈Z.
故选:A.
【考点精析】本题主要考查了函数y=Asin(ωx+φ)的图象变换的相关知识点,需要掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象才能正确解答此题.
的图象才能正确解答此题.

【题目】某地区2010年至2016年农村居民家庭纯收入![]() (单位:千元)的数据如下表
(单位:千元)的数据如下表
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求![]() 关于
关于![]() 的线性回归方程。
的线性回归方程。
(2)判断![]() 与
与![]() 之间是正相关还是负相关?
之间是正相关还是负相关?
(3)预测该地区2018年农村居民家庭人均纯收入。
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
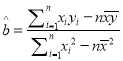 ,
, ![]()