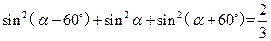题目内容
(本小题满分14分)
如图,某市拟在道路的一侧修建一条运动赛道,赛道的前一部分为曲线段ABC,该曲线段为函数y=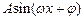 (A>0,
(A>0, >0,
>0, <
< <
< ),x∈[-3,0]的图象,且图象的最高点为B(-1,
),x∈[-3,0]的图象,且图象的最高点为B(-1, );赛道的中间部分为
);赛道的中间部分为 千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧
千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧 .
.

(1)求 ,
, 的值和∠DOE的值;
的值和∠DOE的值;
(2)若要在圆弧赛道所对应的扇形区域内建一个“矩形草坪”,如图所示,矩形的一边在道路AE上,一个顶点在扇形半径OD上.记∠POE= ,求当“矩形草坪”的面积最大时
,求当“矩形草坪”的面积最大时 的值.
的值.
如图,某市拟在道路的一侧修建一条运动赛道,赛道的前一部分为曲线段ABC,该曲线段为函数y=
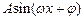 (A>0,
(A>0, >0,
>0, <
< <
< ),x∈[-3,0]的图象,且图象的最高点为B(-1,
),x∈[-3,0]的图象,且图象的最高点为B(-1, );赛道的中间部分为
);赛道的中间部分为 千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧
千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧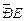 .
.
(1)求
 ,
, 的值和∠DOE的值;
的值和∠DOE的值;(2)若要在圆弧赛道所对应的扇形区域内建一个“矩形草坪”,如图所示,矩形的一边在道路AE上,一个顶点在扇形半径OD上.记∠POE=
 ,求当“矩形草坪”的面积最大时
,求当“矩形草坪”的面积最大时 的值.
的值.解析:(1)依题意,得A= ,
,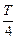 =2,因为T=
=2,因为T=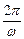 ,所以
,所以 =
=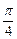 ,所以y=
,所以y= .
.
当x=-1时,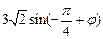 =
= ,由
,由 <
< <
< ,得
,得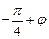 =
= ,所以
,所以 =
=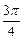 .
.
又x=0时,y=OC=3,因为CD= ,所以∠COD=
,所以∠COD=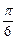 ,从而∠DOE=
,从而∠DOE=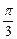 .
.
(2)由(1)可知OD=OP=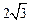 ,“矩形草坪”的面积
,“矩形草坪”的面积
S=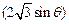
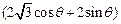 =
=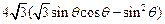
=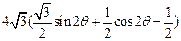 =
=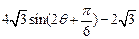 ,
,
其中0< <
<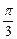 ,所以当
,所以当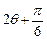 =
= ,即
,即 =
=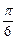 时,S最大.
时,S最大.
 ,
,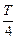 =2,因为T=
=2,因为T=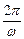 ,所以
,所以 =
=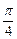 ,所以y=
,所以y= .
.当x=-1时,
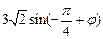 =
= ,由
,由 <
< <
< ,得
,得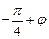 =
= ,所以
,所以 =
=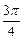 .
.又x=0时,y=OC=3,因为CD=
 ,所以∠COD=
,所以∠COD=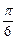 ,从而∠DOE=
,从而∠DOE=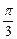 .
.(2)由(1)可知OD=OP=
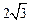 ,“矩形草坪”的面积
,“矩形草坪”的面积S=
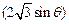
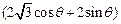 =
=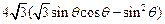
=
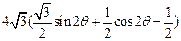 =
=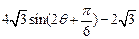 ,
,其中0<
 <
<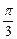 ,所以当
,所以当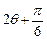 =
= ,即
,即 =
=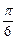 时,S最大.
时,S最大.略

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
 ,
, ,
,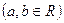
 时,若
时,若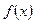 在
在 上单调递增,求
上单调递增,求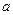 的取值范围;
的取值范围; :当
:当 ,使得
,使得 是
是 是
是 的最小值;
的最小值;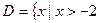 ,且
,且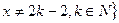 上的函数
上的函数 ,使当
,使当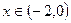 时,
时, ,当
,当 时,
时, 是一个三次函数,
是一个三次函数,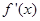 为其导函数.如图所示是函数
为其导函数.如图所示是函数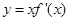 的图像的一部分,则
的图像的一部分,则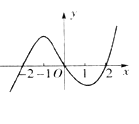
 与
与
 与
与
 ,其图象在
,其图象在 处的切线方程为
处的切线方程为 .
. 的解析式;
的解析式; 的图象与
的图象与 的图象有三个不同的交点,求实数
的图象有三个不同的交点,求实数 的取值范围;
的取值范围;
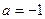 时,求函数的单调区间。
时,求函数的单调区间。 时,讨论函数的单调增区间。
时,讨论函数的单调增区间。 ,使
,使 ,函数有最小值-3?
,函数有最小值-3? 是函数
是函数 的一个极值点,其中
的一个极值点,其中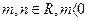
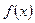 的单调区间
的单调区间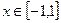 时函数
时函数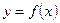 的图象上一任意点的切线斜率恒大于3m,求m的取值范围
的图象上一任意点的切线斜率恒大于3m,求m的取值范围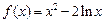 .
.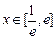 时,不等式
时,不等式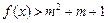 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;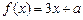 在区间[
在区间[ 1,3]上恰好有两个相异的实根,求实数
1,3]上恰好有两个相异的实根,求实数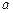 的取值范围.
的取值范围. +
+ +
+ =
= ,
, +
+ +
+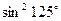 =
=