题目内容
11．已知函数f（x）=x2-ax-b（a，b∈R）的值域为[0，+∞），若关于x的不等式f（x）＜c的解集为（m-3，m+1），则实数c的值为4．分析 根据函数的值域求出a与b的关系，然后根据不等式的解集可得f（x）=c的两个根为m-3，m+1最后利用根与系数的关系建立等式，解之即可．
解答 解：∵函数f（x）=x2-ax-b（a，b∈R）的值域为[0，+∞），
∴f（x）=0只有一个根，即△=a2+4b=0，则b=-$\frac{{a}^{2}}{4}$，
不等式f（x）＜c的解集为（m-3，m+1），
即为x2-ax+$\frac{{a}^{2}}{4}$＜c解集为（m-3，m+1），
则x2-ax+$\frac{{a}^{2}}{4}$-c=0的两个根为m-3，m+1，
∴m-3+m+1=2m-2=a，（m-3）•（m+1）=m2-2m-3=$\frac{{a}^{2}}{4}$-c，
解得：c=4，
故答案为：4．
点评 本题主要考查了一元二次不等式的应用，以及根与系数的关系，同时考查了分析求解的能力和计算能力，属于中档题．
练习册系列答案
相关题目
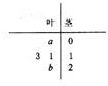如图所示是某组数据的茎叶图，已知该组数据的平均数为$\frac{23}{2}$，ab=1（a，b∈R），则$\frac{a}{2}sin2x+bco{s}^{2}x-\frac{b}{2}$的最大值为$\frac{\sqrt{2}}{2}$．
6．已知f（x）=10x，g（x）=2x，x0＜0，则（ ）
| A． | 1＞f（x0）＞g（x0） | B． | 1＞g（x0）＞f（x0） | C． | f（x0）＞g（x0）＞1 | D． | g（x0）＞f（x0）＞2 |