题目内容
7. 已知椭圆$\frac{x^2}{16}+\frac{y^2}{b^2}$=1(0<b<4),点C(8,0),直线AC和椭圆相交于不重合的两点A、B(直线AC不与x轴重合),从A点出发的光线经x轴反射后过点B,设A(m,n),如图所示.
已知椭圆$\frac{x^2}{16}+\frac{y^2}{b^2}$=1(0<b<4),点C(8,0),直线AC和椭圆相交于不重合的两点A、B(直线AC不与x轴重合),从A点出发的光线经x轴反射后过点B,设A(m,n),如图所示.(Ⅰ)写出直线AC的方程.
(Ⅱ)求证点B的坐标是($\frac{5m-16}{m-5}$,-$\frac{3n}{m-5}$).
(Ⅲ)求x轴上光线反射点D的坐标.
分析 (Ⅰ)通过点C(8,0)在椭圆外,及A(m,n),利用点斜式方程可得直线AC的方程;
(Ⅱ)联立直线AC及椭圆方程,结合A(m,n),再设B(x0,y0),通过韦达定理即可得结论;
(III)由对称性知点A关于x轴的对称点A′(m,-n)也在椭圆上,从而直线A′B与x轴的交点就是光线反射点D,计算可得直线A′B的方程,令其y=0即可.
解答  (Ⅰ)解:∵点C(8,0)在椭圆外,∴直线AC斜率存在.
(Ⅰ)解:∵点C(8,0)在椭圆外,∴直线AC斜率存在.
∵A(m,n),∴直线AC斜率为$\frac{n}{m-8}$,
∴直线AC的方程是$y=\frac{n}{m-8}(x-8)$;
(Ⅱ)证明:由方程组$\left\{\begin{array}{l}{y=\frac{n}{m-8}(x-8)}\\{\frac{{x}^{2}}{16}+\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$,
得(b2m2-16b2m+64b2+16n2)x2-162n2x+16×64n2-16b2(m-8)2=0,
∵A(m,n)在椭圆$\frac{x^2}{16}+\frac{y^2}{b^2}$=1上,∴$\frac{{m}^{2}}{16}+\frac{{n}^{2}}{{b}^{2}}=1$,即b2m2+16n2=16b2,
∴(80b2-16b2m)x2-162n2x+16×64n2-16b2(m-8)2=0.
设B(x0,y0),则有${x}_{0}+m=\frac{1{6}^{2}{n}^{2}}{80{b}^{2}-16{b}^{2}m}$,
∴x0=$\frac{1{6}^{2}{n}^{2}}{80{b}^{2}-16{b}^{2}m}-m$=$\frac{16(16{n}^{2}+{b}^{2}{m}^{2})-80{b}^{2}m}{80{b}^{2}-16{b}^{2}m}$=$\frac{16{b}^{2}-5{b}^{2}m}{5{b}^{2}-{b}^{2}m}$=$\frac{5m-16}{m-5}$,
∴${y_0}=\frac{n}{m-8}({x_0}-8)=\frac{n}{m-8}(\frac{5m-16}{m-5}-8)=-\frac{3n}{m-5}$,
∴点B的坐标是($\frac{5m-16}{m-5}$,-$\frac{3n}{m-5}$);
(III)解:由椭圆的对称性知,点A关于x轴的对称点A′(m,-n)也在椭圆上.
根据光学知识,直线A′B与x轴的交点就是光线反射点D,如图所示.
∵A、B两点不重合,∴直线A′B的斜率为$\frac{-\frac{3n}{m-5}+n}{\frac{5m-16}{m-5}-m}=-\frac{n}{m-2}$,
∴直线A′B的方程是$y+n=-\frac{n}{m-2}(x-m)$,
∵直线AC不与x轴重合,∴n≠0,
∴在直线A′B的方程中令y=0,得x=2,
∴轴上光线反射点D的坐标为(2,0).
点评 本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查韦达定理的运用,考查学生的计算能力,属于中档题.

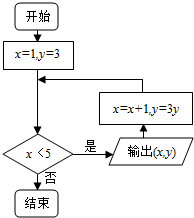
| A. | y=x+2图象上 | B. | y=3x图象上 | C. | y=3x的图象上 | D. | y=3x3图象上 |
