ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐyΘΫf1Θ®xΘ©Θ§yΘΫf2Θ®xΘ©Θ§Ε®“εΚ· ΐfΘ®xΘ© Θ°
Θ°
Θ®1Θ©…ηΚ· ΐf1Θ®xΘ©ΘΫx+3Θ§f2Θ®xΘ©ΘΫx2©¹xΘ§«σΚ· ΐyΘΫfΘ®xΘ©ΒΡΫβΈω ΫΘΜ
Θ®2Θ©‘ΎΘ®1Θ©ΒΡΧθΦΰœ¬Θ§gΘ®xΘ©ΘΫmx+2Θ®mΓ RΘ©Θ§Κ· ΐhΘ®xΘ©ΘΫfΘ®xΘ©©¹gΘ®xΘ©”–»ΐΗω≤ΜΆ§ΒΡΝψΒψΘ§«σ Β ΐmΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®3Θ©…ηΚ· ΐf1Θ®xΘ©ΘΫx2©¹2Θ§f2Θ®xΘ©ΘΫ|x©¹a|Θ§Κ· ΐFΘ®xΘ©ΘΫf1Θ®xΘ©+f2Θ®xΘ©Θ§«σΚ· ΐFΘ®xΘ©ΒΡΉν–Γ÷ΒΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©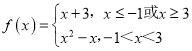 ΘΜΘ®2Θ©
ΘΜΘ®2Θ©![]() ΘΜΘ®3Θ©
ΘΜΘ®3Θ©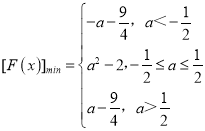
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΚ· ΐfΘ®xΘ©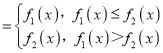 ΒΡΕ®“εΘ§ΝΫΗωΚ· ΐ÷–»Γ–ΓΒΡ.
ΒΡΕ®“εΘ§ΝΫΗωΚ· ΐ÷–»Γ–ΓΒΡ.
Θ®2Θ©Κ· ΐhΘ®xΘ©ΘΫfΘ®xΘ©©¹gΘ®xΘ©”–»ΐΗω≤ΜΆ§ΒΡΝψΒψΘ§Φ¥ΖΫ≥ΧfΘ®xΘ©ΘΫgΘ®xΘ©”–»ΐΗω≤ΜΆ§ΒΡ Β ΐΗυΘ§“ρΈΣΚ· ΐ![]() «Ζ÷ΕΈΚ· ΐΘ§Ζ÷άύΧ÷¬έΘ§Ζ÷±π”Ο“Μ¥ΈΖΫ≥ΧΚΆΕΰ¥ΈΖΫ≥Χ«σΫβ.
«Ζ÷ΕΈΚ· ΐΘ§Ζ÷άύΧ÷¬έΘ§Ζ÷±π”Ο“Μ¥ΈΖΫ≥ΧΚΆΕΰ¥ΈΖΫ≥Χ«σΫβ.
Θ®3Θ©ΗυΨίΧβ“βFΘ®xΘ©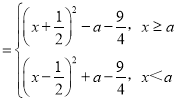 Θ°Α¥’’Εΰ¥ΈΚ· ΐΚ· ΐΕ®«χΦδΕ·ΒΡάύ–ΆΘ§Χ÷¬έΕ‘≥Τ÷α”κ«χΦδΕΥΒψ÷ΒΦδΒΡΙΊœΒ«σΉν÷Β.
Θ°Α¥’’Εΰ¥ΈΚ· ΐΚ· ΐΕ®«χΦδΕ·ΒΡάύ–ΆΘ§Χ÷¬έΕ‘≥Τ÷α”κ«χΦδΕΥΒψ÷ΒΦδΒΡΙΊœΒ«σΉν÷Β.
Θ®1Θ©ΓΏf1Θ®xΘ©ΘΫx+3Θ§![]() Θ§
Θ§
Β±f1Θ®xΘ©Γήf2Θ®xΘ©Θ§Φ¥xΓί3ΜρxΓή©¹1 ±Θ§fΘ®xΘ©ΘΫx+3Θ§
Β±f1Θ®xΘ©ΘΨf2Θ®xΘ©Θ§Φ¥©¹1ΘΦxΘΦ3 ±Θ§![]() Θ§
Θ§
Ήέ…œΘΚ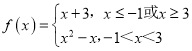 Θ°
Θ°
Θ®2Θ©Κ· ΐhΘ®xΘ©ΘΫfΘ®xΘ©©¹gΘ®xΘ©”–»ΐΗω≤ΜΆ§ΒΡΝψΒψΘ§
Φ¥ΖΫ≥ΧfΘ®xΘ©ΘΫgΘ®xΘ©”–»ΐΗω≤ΜΆ§ΒΡ Β ΐΗυΘ§
“ρΈΣΚ· ΐ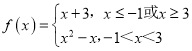 Θ§Κ· ΐgΘ®xΘ©ΘΫmx+2Θ®mΓ RΘ©Θ§
Θ§Κ· ΐgΘ®xΘ©ΘΫmx+2Θ®mΓ RΘ©Θ§
Υυ“‘Β±xΓή©¹1ΜρxΓί3 ±Θ§mx+2ΘΫx+3«Γ”–“ΜΗω Β ΐΫβΘ§
Υυ“‘![]() Μρ
Μρ![]() Θ§
Θ§
ΫβΒΟΘ§![]() Θ°
Θ°
Β±©¹1ΘΦxΘΦ3 ±Θ§mx+2ΘΫx2©¹x«Γ”–ΝΫΗω≤ΜΆ§ΒΡ Β ΐΫβΘ§
Φ¥Β±©¹1ΘΦxΘΦ3 ±x2©¹Θ®m+1Θ©x©¹2=0«Γ”–ΝΫΗω≤ΜΆ§ΒΡ Β ΐΫβΘ§
…ηΚ· ΐhΘ®xΘ©ΘΫx2©¹Θ®m+1Θ©x©¹2Θ§
”…Χβ“βΩ…ΒΟ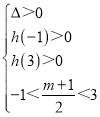 Θ§
Θ§
Υυ“‘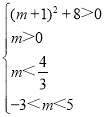 Θ§
Θ§
ΫβΒΟ![]() Θ§
Θ§
Ήέ…œΘ§mΒΡ»Γ÷ΒΖΕΈßΈΣ![]() Θ°
Θ°
Θ®3Θ©FΘ®xΘ©ΘΫf1Θ®xΘ©+f2Θ®xΘ©ΘΫx2+|x©¹a|©¹2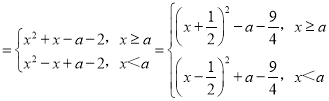 Θ°
Θ°
ΔΌ»τa![]() Θ§‘ρΚ· ΐFΘ®xΘ©‘Ύ
Θ§‘ρΚ· ΐFΘ®xΘ©‘Ύ![]() …œ «ΒΞΒςΦθΚ· ΐΘ§‘Ύ
…œ «ΒΞΒςΦθΚ· ΐΘ§‘Ύ![]() …œ «ΒΞΒς‘ωΚ· ΐΘ§
…œ «ΒΞΒς‘ωΚ· ΐΘ§
¥Υ ±Θ§Κ· ΐFΘ®xΘ©ΒΡΉν–Γ÷ΒΈΣ![]() ΘΜ
ΘΜ
ΔΎ»τ![]() Θ§‘ρΚ· ΐFΘ®xΘ©‘ΎΘ®©¹ΓόΘ§aΘ©…œ «ΒΞΒςΦθΚ· ΐΘ§‘ΎΘ®aΘ§+ΓόΘ©…œ «ΒΞΒς‘ωΚ· ΐΘ§
Θ§‘ρΚ· ΐFΘ®xΘ©‘ΎΘ®©¹ΓόΘ§aΘ©…œ «ΒΞΒςΦθΚ· ΐΘ§‘ΎΘ®aΘ§+ΓόΘ©…œ «ΒΞΒς‘ωΚ· ΐΘ§
¥Υ ±Θ§Κ· ΐFΘ®xΘ©ΒΡΉν–Γ÷ΒΈΣFΘ®aΘ©ΘΫa2©¹2ΘΜ
Δέ»τ![]() Θ§‘ρΚ· ΐFΘ®xΘ©‘Ύ
Θ§‘ρΚ· ΐFΘ®xΘ©‘Ύ![]() …œ «ΒΞΒςΦθΚ· ΐΘ§‘Ύ
…œ «ΒΞΒςΦθΚ· ΐΘ§‘Ύ![]() …œ «ΒΞΒς‘ωΚ· ΐΘ§
…œ «ΒΞΒς‘ωΚ· ΐΘ§
¥Υ ±Θ§Κ· ΐFΘ®xΘ©ΒΡΉν–Γ÷ΒΈΣ![]() ΘΜ
ΘΜ
Ήέ…œΘΚ Θ°
Θ°

ΓΨΧβΡΩΓΩΫϋΤΎΘ§Ρ≥―ß–ΘΨΌ––ΝΥ“Μ¥ΈΧε”ΐ÷Σ ΕΨΚ»ϋΘ§≤ΔΕ‘ΨΚ»ϋ≥…Φ®Ϋχ––Ζ÷ΉιΘΚ≥…Φ®≤ΜΒΆ”Ύ80Ζ÷ΒΡ―ß…ζΈΣΦΉΉιΘ§≥…Φ®ΒΆ”Ύ80Ζ÷ΒΡ―ß…ζΈΣ““Ήι.ΈΣΝΥΖ÷ΈωΨΚ»ϋ≥…Φ®”κ–‘±π «Ζώ”–ΙΊΘ§œ÷ΥφΜζ≥ι»ΓΝΥ60Οϊ―ß…ζΒΡ≥…Φ®Ϋχ––Ζ÷ΈωΘ§ ΐΨί»γœ¬ΆΦΥυ ΨΒΡ![]() Ν–ΝΣ±μ.
Ν–ΝΣ±μ.
ΦΉΉι | ““Ήι | ΚœΦΤ | |
Ρ–…ζ | 3 | ||
≈°…ζ | 13 | ||
ΚœΦΤ | 40 | 60 |
Θ®1Θ©ΫΪ![]() Ν–ΝΣ±μ≤Ι≥δΆξ’ϊΘ§≈–Εœ «Ζώ”–
Ν–ΝΣ±μ≤Ι≥δΆξ’ϊΘ§≈–Εœ «Ζώ”–![]() ΒΡΑ―Έ’»œΈΣ―ß…ζΑ¥≥…Φ®Ζ÷Ήι”κ–‘±π”–ΙΊΘΩ
ΒΡΑ―Έ’»œΈΣ―ß…ζΑ¥≥…Φ®Ζ÷Ήι”κ–‘±π”–ΙΊΘΩ
Θ®2Θ©»γΙϊ”ΟΖ÷≤ψ≥ι―υΒΡΖΫΖ®¥”ΦΉΉιΚΆ““Ήι÷–≥ι»Γ6»ΥΘ§‘Ό¥”’β6»Υ÷–ΥφΜζ≥ι»Γ2»ΥΘ§«σ÷Ν…Ό”–1»Υ‘ΎΦΉΉιΒΡΗ≈¬ .
ΗΫΘΚ Θ§
Θ§![]() .
.
≤ΈΩΦ ΐΨίΦΑΙΪ ΫΘΚ
| 0.100 | 0.050 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
ΓΨΧβΡΩΓΩΥφΉ≈Έ“ΙζΨ≠ΦΟΒΡΖΔ’ΙΘ§Ψ”Οώ ’»κ÷πΡξ‘ω≥ΛΘ°Ρ≥ΒΊ«χ2014Ρξ÷Ν2018Ρξ≈©¥εΨ”ΟώΦ“ΆΞ»ΥΨυ¥Ω ’»κ![]() Θ®ΒΞΈΜΘΚ«ß‘ΣΘ©ΒΡ ΐΨί»γœ¬±μΘΚ
Θ®ΒΞΈΜΘΚ«ß‘ΣΘ©ΒΡ ΐΨί»γœ¬±μΘΚ
ΡξΖί | 2014 | 2015 | 2016 | 2017 | 2018 |
ΡξΖί¥ζΚ≈ | 1 | 2 | 3 | 4 | 5 |
»ΥΨυ¥Ω ’»κ | 5 | 6 | 7 | 8 | 10 |
Θ®1Θ©«σ![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΘΜ
ΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΘΜ
Θ®2Θ©άϊ”ΟΘ®1Θ©÷–ΒΡΜΊΙιΖΫ≥ΧΘ§Ζ÷Έω2014Ρξ÷Ν2018ΡξΗΟΒΊ«χ≈©¥εΨ”ΟώΦ“ΆΞ»ΥΨυ¥Ω ’»κΒΡ±δΜ·«ιΩωΘ§≤Δ‘Λ≤β2020ΡξΗΟΒΊ«χ≈©¥εΨ”ΟώΦ“ΆΞ»ΥΨυ¥Ω ’»κ‘ΦΈΣΕύ…Ό«ß‘ΣΘΩ
ΗΫΘΚΜΊΙι÷±œΏΒΡ–±¬ ΚΆΫΊΨύΒΡΉν–ΓΕΰ≥ΥΙάΦΤΙΪ ΫΖ÷±πΈΣ Θ§
Θ§![]() .
.
