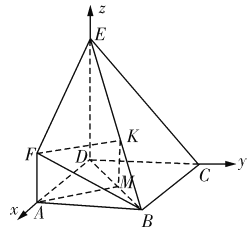
题目内容
【题目】如图,![]() 是边长为3的正方形,
是边长为3的正方形,![]() 平面
平面![]() ,
,![]() ,且
,且![]() ,
,![]() .
.
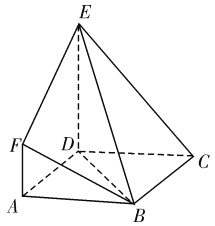
(1)试在线段![]() 上确定一点
上确定一点![]() 的位置,使得
的位置,使得![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】分析:(1)设平面ACF与BD交于点M,与BE交于点N,M点就量所求,由此可知M是BD的三等分点中靠近B点的一个,由线面平行的判定定理可证;
(2)分别以DA,DC,DE为![]() 轴建立空间直角坐标系,写出各点坐标,求出平面ABE和平面CBE的法向量,由法向量的夹角可得所求二面角.
轴建立空间直角坐标系,写出各点坐标,求出平面ABE和平面CBE的法向量,由法向量的夹角可得所求二面角.
详解:(1)证明:取![]() 的三等分点
的三等分点![]() (靠近点
(靠近点![]() ),过
),过![]() 作
作![]() 交
交![]() 于
于![]() ,则有
,则有![]() ,由
,由![]() 平面
平面![]() ,
,![]() ,可知
,可知![]() 平面
平面![]() ,
,
∴![]() ,∴
,∴![]() ,且
,且![]() .
.
∴四边形![]() 为平行四边形,可知
为平行四边形,可知![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() ,∴
,∴![]() 为
为![]() 的一个三等分点(靠近点
的一个三等分点(靠近点![]() ).
).
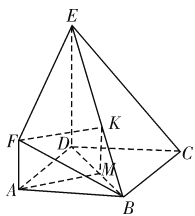
(2)如图建立空间直角坐标系:则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,由
,由![]() 可得
可得![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,由
,由![]() 可得
可得![]() ,
,
因为二面角![]() 为钝二面角,可得
为钝二面角,可得![]() ,
,
所以二面角![]() 余弦值为
余弦值为![]() .
.

练习册系列答案
相关题目
【题目】为了引导居民合理用水,某市决定全面实施阶梯水价.阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价,具体划分标准如表:
阶梯级别 | 第一阶梯水量 | 第二阶梯水量 | 第三阶梯水量 |
月用水量范围(单位:立方米) |
|
|
|
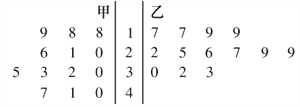
从本市随机抽取了10户家庭,统计了同一月份的月用水量,得到如图茎叶图:

(1)现要在这10户家庭中任意选取3家,求取到第二阶梯水量的户数![]() 的分布列与数学期望;
的分布列与数学期望;
(2)用抽到的10户家庭作为样本估计全市的居民用水情况,从全市依次随机抽取10户,若抽到![]() 户月用水量为二阶的可能性最大,求
户月用水量为二阶的可能性最大,求![]() 的值.
的值.