Question

【题目】设函数f（x）=3sinx+2cosx+1．若实数a，b，c使得af（x）+bf（x﹣c）=1对任意实数x恒成立，则 的值为（ ）
A.﹣1
B.
C.1
D.

Answer 1

【答案】A
【解析】解：由题设可得f（x）= sin（x+θ）+1，f（x﹣c）= sin（x+θ﹣c）+1，其中cosθ= ，sinθ= （0＜θ＜ ），
∴af（x）+bf（x﹣c）=1可化成 asin（x+θ）+ bsin（x+θ﹣c）+a+b=1，
即 （a+bcosc）sin（x+θ）﹣ bsinccos（x+θ）+（a+b﹣1）=0，
由已知条件，上式对任意x∈R恒成立，故必有 ，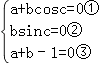
若b=0，则式（1）与式（3）矛盾；
故此b≠0，由（2）式得到：sinc=0，
当cosc=1时，有矛盾，故cosc=﹣1，
由①③知a=b= ，
则 =﹣1．
故选A
【考点精析】解答此题的关键在于理解两角和与差的正弦公式的相关知识，掌握两角和与差的正弦公式：．