题目内容
(12分)已知圆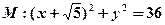 及定点
及定点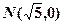 ,点
,点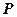 是圆
是圆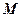 上的动点,
上的动点,
点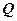 在
在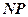 上,点
上,点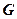 在
在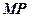 上,且满足
上,且满足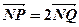 ,
,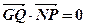 .
.
(1)求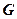 的轨迹
的轨迹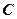 的方程;
的方程;
(2)过点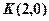 作直线
作直线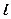 ,与曲线
,与曲线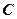 交于
交于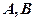 两点,
两点,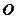 为坐标原点,设
为坐标原点,设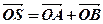 ,是否存在这样的直线
,是否存在这样的直线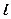 ,使四边形
,使四边形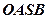 的对角线相等?若存在,求出直线
的对角线相等?若存在,求出直线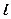 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
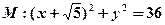 及定点
及定点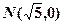 ,点
,点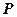 是圆
是圆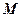 上的动点,
上的动点,点
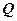 在
在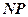 上,点
上,点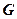 在
在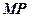 上,且满足
上,且满足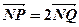 ,
,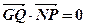 .
.(1)求
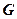 的轨迹
的轨迹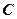 的方程;
的方程;(2)过点
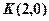 作直线
作直线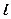 ,与曲线
,与曲线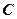 交于
交于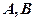 两点,
两点,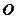 为坐标原点,设
为坐标原点,设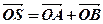 ,是否存在这样的直线
,是否存在这样的直线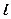 ,使四边形
,使四边形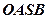 的对角线相等?若存在,求出直线
的对角线相等?若存在,求出直线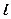 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.(1)

(2)
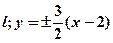
(1) ,所以椭圆方程为
,所以椭圆方程为
(2) 四边形
四边形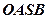 为平行四边形,又其对角线相等,则
为平行四边形,又其对角线相等,则
当直线的斜率不存在时,四边形的对角线不相等;
当直线的斜率存在时,设直线 ,联立
,联立


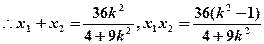
 ,
,
整理得 (*)
(*)
代入得
所以存在直线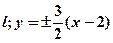
 ,所以椭圆方程为
,所以椭圆方程为
(2)
 四边形
四边形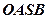 为平行四边形,又其对角线相等,则
为平行四边形,又其对角线相等,则
当直线的斜率不存在时,四边形的对角线不相等;
当直线的斜率存在时,设直线
 ,联立
,联立

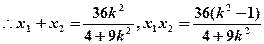
 ,
,整理得
 (*)
(*)代入得

所以存在直线
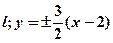

练习册系列答案
相关题目
 :
: 与圆
与圆 :
: 的位置关系是
的位置关系是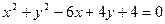 .
.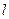 过点P且与圆心C的距离为1,求直线
过点P且与圆心C的距离为1,求直线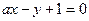 与圆C交于A、B两点,是否存在实数
与圆C交于A、B两点,是否存在实数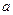 ,使得过点P(2,0)的直线
,使得过点P(2,0)的直线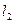 垂直平
垂直平 相外切,且与线
相外切,且与线 相切于点
相切于点 的圆的方程.
的圆的方程.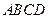 是圆
是圆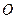 的内接四边形,延长
的内接四边形,延长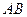 和
和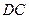 相交于点
相交于点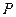 ,若
,若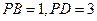 ,则
,则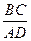 的值为 .
的值为 .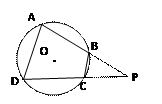
 与圆
与圆 的公共弦长为
的公共弦长为 ,a=_______
,a=_______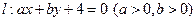 始终平分圆
始终平分圆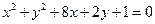 ,则
,则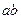 的最大值为( )
的最大值为( )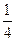
 ,
, 满足
满足 ,那么
,那么 的取值范围是
的取值范围是