题目内容
16.数列{an}与{bn}中,an=n2+2n,bn•an=2,则b1+b2+…+b18=$\frac{431}{380}$.分析 an=n2+2n,bn•an=2,可得bn=$\frac{2}{{a}_{n}}$=$\frac{2}{{n}^{2}+2n}$=$\frac{1}{n}-\frac{1}{n+2}$.利用“裂项求和”即可的得出.
解答 解:∵an=n2+2n,bn•an=2,
∴bn=$\frac{2}{{a}_{n}}$=$\frac{2}{{n}^{2}+2n}$=$\frac{1}{n}-\frac{1}{n+2}$.
则b1+b2+…+b18=$(1-\frac{1}{3})+(\frac{1}{2}-\frac{1}{4})$+$(\frac{1}{3}-\frac{1}{5})$+…+$(\frac{1}{17}-\frac{1}{19})$+$(\frac{1}{18}-\frac{1}{20})$
=1+$\frac{1}{2}$-$\frac{1}{19}-\frac{1}{20}$
=$\frac{431}{380}$.
故答案为:$\frac{431}{380}$.
点评 本题考查了“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
9.若2=Z(1-i),则Z=( )
| A. | 1 | B. | 1-i | C. | 1+i | D. | -i |
4.点P(x0,y0)在直线l:f(x,y)=0外,则l1:f(x,y)+f(x0,y0)=0与l2:f(-y,x)+f(x0,y0)=0的位置关系是( )
| A. | 平行 | B. | 垂直 | C. | 平行或重合 | D. | 相交且不垂直 |
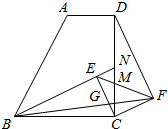 在四边形ABCD中,AD∥BC,BC=CD,∠ADC=90°,BC=DC=2AD,E为四边形ABCD内一点,F为四边形ABCD外一点,且∠BEC=∠DFC=90°,BE∥CF交CD的中点于N.
在四边形ABCD中,AD∥BC,BC=CD,∠ADC=90°,BC=DC=2AD,E为四边形ABCD内一点,F为四边形ABCD外一点,且∠BEC=∠DFC=90°,BE∥CF交CD的中点于N.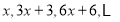 的第四项等于( )
的第四项等于( )