题目内容
（本小题满分14分）
如图所示，在长方体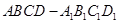
中，AB=AD=1，AA1=2，M是棱CC1的中点
（Ⅰ）求异面直线A1M和C1D1所成的角的正切值；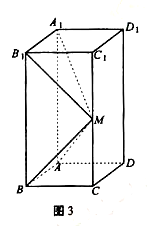
（Ⅱ）证明：平面ABM⊥平面A1B1M1
解析
练习册系列答案
名校课堂系列答案
相关题目
名校课堂系列答案题目内容
（本小题满分14分）
如图所示，在长方体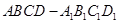中，AB=AD=1，AA1=2，M是棱CC1的中点
（Ⅰ）求异面直线A1M和C1D1所成的角的正切值；
（Ⅱ）证明：平面ABM⊥平面A1B1M1
解析
名校课堂系列答案
;
，∠ACB＝900，M是AA1的中点，N是BC1的中点．
中，
分别为
的中点。
平面
；
平面
，且
，
，求证：平面
平面
。
⊥平面
,
,
,
与直线
所成的角为
，又
。 
；
的余弦值
BC，CD，DB分别将△BCA2，△CDA3，△DBA1翻折上去恰好使A1，A2，A3重合于一点A。
中，侧棱
平面
，底面
，
，
，
分别是
的中点．
平面
与底面
时，求二面角
的大小．
，
〉的值为( )
，
，0)，点D在平面yOz上，且∠BDC＝90°，∠DCB＝30°，则AD的长度为( )
