题目内容
如图，在正三棱柱ABC—A1B1C1中，底面边长及侧棱长均为2，D是棱AB的中点，
(1)求证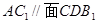
;
(2)求异面直线AC1与B1C所成角的余弦值. 
（1）证明见解析；（2）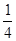
。
解析
练习册系列答案
全能测控一本好卷系列答案
相关题目
全能测控一本好卷系列答案题目内容
如图，在正三棱柱ABC—A1B1C1中，底面边长及侧棱长均为2，D是棱AB的中点，
(1)求证;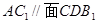
(2)求异面直线AC1与B1C所成角的余弦值.
（1）证明见解析；（2）。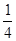
解析
全能测控一本好卷系列答案
中，
底面
，
，
，
，
是
的中点．
；
平面
；
的正切值．
中，
、
分别是
、
的中点，点
在
上，
. 
平面
.
中，侧面
与侧面
均为等边三角形，
，
为
中点．
平面
；
的余弦值．
中，
，
是
和
的中点.（Ⅰ）求证：
平面
;
,求
中，
，
为
中点.
；
上是否存在一点
，使得
平面
？若存在，求
的长；若不存在，说明理由.
的大小为
，求
的长.
中，所有的棱长都为2，
.
；
与平面
所成的锐角的余弦值.
中，底面
为矩形，
⊥底面
，点
是棱
的中点. 
到平面
的距离；
，求二面角
的平面角的余弦值 .
中，AB=AD=1，AA1=2，M是棱CC1的中点