题目内容
已知函数f(x)是以2为周期的偶函数,且当x∈(0,1)时,f(x)=2x-1,则f(log210)的值为 .
考点:函数的周期性,函数奇偶性的性质
专题:函数的性质及应用
分析:由函数的周期性与奇偶性把f(log210)转化为求f(log2
)得答案.
| 8 |
| 5 |
解答:
解:∵f(x)是以2为周期的偶函数,且当x∈(0,1)时,f(x)=2x-1,
∴f(log210)=f(log210-4)=f(log210-log216)
=f(log2
)=f(log2
)=f(log2
)
=2log2
-1=
.
故答案为:
.
∴f(log210)=f(log210-4)=f(log210-log216)
=f(log2
| 10 |
| 16 |
| 5 |
| 8 |
| 8 |
| 5 |
=2log2
| 8 |
| 5 |
| 3 |
| 5 |
故答案为:
| 3 |
| 5 |
点评:本题考查了函数的周期性与奇偶性的性质,考查了数学转化思想方法,是基础题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
若等边△ABC的边长为2
,平面内一点M满足
=
+
,则
•
=( )
| 3 |
| CM |
| 1 |
| 6 |
| CB |
| 2 |
| 3 |
| CA |
| MA |
| MB |
| A、1 | B、2 | C、-1 | D、-2 |
已知sin(π-α)=-
,且α是第四象限的角,那么cosα的值是( )
| 3 |
| 5 |
A、-
| ||
B、
| ||
C、±
| ||
D、
|
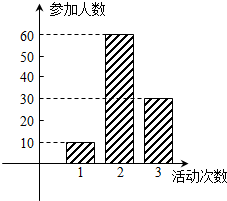 某中学号召学生在暑假期间至少参加一次社会公益活动,该校文学社有100名学生,他们参加活动的次数统计如图所示,求:
某中学号召学生在暑假期间至少参加一次社会公益活动,该校文学社有100名学生,他们参加活动的次数统计如图所示,求: