题目内容
10.已知抛物线与y轴交于点A(0,-3),与x轴的两个交点的横坐标为方程x2+2x-3=0的两根,求它的解析式、顶点坐标和对称轴方程.分析 利用已知条件设出抛物线方程,求出方程的根,然后求解函数的解析式,顶点坐标和对称轴方程.
解答 解:抛物线与y轴交于点A(0,-3),
设抛物线方程为:y=ax2+bx-3,
解方程x2+2x-3=0得x1=1,x2=-3.
根据题意,又设抛物线解析式为y=a(x-1)(x+3)=ax2+2ax-3a,
可得a=1,b=2
∴解析式为y=x2+2x-3=(x+1)2-4.
顶点坐标为(-1,-4),对称轴为x=-1.
点评 此题考查了运用待定系数法求函数解析式进而求解,二次函数的简单性质的应用,属基础题.

练习册系列答案
相关题目
5.下列说法中正确的是( )
| A. | 命题“?x∈R,ex>0”的否定是“?x∈R,ex>0” | |
| B. | 命题“已知x,y∈R,若x+y≠3,则x≠2或y≠1”是真命题 | |
| C. | “x2+2x≥ax在x∈[1,2]上恒成立”?“对于x∈[1,2],有(x2+2x)min≥(ax)max” | |
| D. | 命题“若a=-1,则函数f(x)=ax2+2x-1只有一个零点”的逆命题为真命题 |
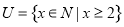 ,集合
,集合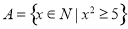 ,则
,则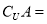 ( )
( ) B.
B.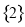 C.
C.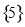 D.
D.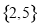
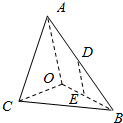 如图,在三棱锥A-BOC中,AO⊥平面COB,∠OAB=∠OAC=$\frac{π}{6}$,AB=AC=2,BC=$\sqrt{2}$,D,E分别为AB,OB的中点.
如图,在三棱锥A-BOC中,AO⊥平面COB,∠OAB=∠OAC=$\frac{π}{6}$,AB=AC=2,BC=$\sqrt{2}$,D,E分别为AB,OB的中点.