题目内容
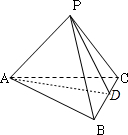
如图所示三棱锥P-ABC中，异面直线PA与BC所成的角为90°，二面角P-BC-A为60°，△PBC和△ABC的面积分别为16和10，BC=4．
求：（1）PA的长；
（2）三棱锥P-ABC的体积VP-ABC．
求：（1）PA的长；
（2）三棱锥P-ABC的体积VP-ABC．
（1）作AD⊥BC于D，连PD，由已知PA⊥BC，∴BC⊥面PAD，∴BC⊥PD，∴∠PDA为二面角
的平面角，∴∠PDF=60°，可算出PD=8，AD=5，∴PA=
=7．
（2）V=
×
PD•ADsin60°•BC=
×
×8×5×
×4=
的平面角，∴∠PDF=60°，可算出PD=8，AD=5，∴PA=
| AD2+DP2-2AD•PDcos60° |
（2）V=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
40
| ||
| 3 |
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
AB，点P在平面ABCD上，且动点P到直线A1D1的距离的平方与P到点M的距离的平方差为1，在平面直角坐标系xAy中，动点P的轨迹方程是 . 
