题目内容
【题目】设函数
，则下列结论不正确的是（ ）
A.函数
在区间
上单调递增
B.函数在区间
上单调递减
C.函数的极大值是
，极小值是
D.存在某一个实数
的值，使得函数是偶函数
【答案】D
【解析】
利用导数可得函数的单调性和极值，可知A，B，C项都是正确的，可以排除A，B，C项，假设存在实数
的值，使得数
是偶函数，推出矛盾，故D项错误.
因为
，所以
．令
，得
或
；
令
，得
；令
，得
或
，
所以函数在区间
和
上单调递增，在区间
上单调递减．故A，B项都是正确的，排除A、B项；
根据单调性易知，函数在处取得极大值，在处取得极小值，所以函数的极大值是
，极小值是
，故C项都是正确的，排除C项；
假设存在实数的值，使得数是偶函数，则由
对任意
恒成立，得
对任意恒成立，这显然不可能，所以不存在实数的值，使得数是偶函数．故D项错误．
故选：D．
练习册系列答案
相关题目
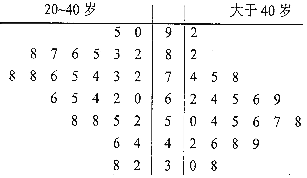
【题目】某公司即将推车一款新型智能手机，为了更好地对产品进行宣传，需预估市民购买该款手机是否与年龄有关，现随机抽取了50名市民进行购买意愿的问卷调查，若得分低于60分，说明购买意愿弱；若得分不低于60分，说明购买意愿强，调查结果用茎叶图表示如图所示．
（1）根据茎叶图中的数据完成
列联表，并判断是否有95%的把握认为市民是否购买该款手机与年龄有关？
购买意愿强 | 购买意愿弱 | 合计 | |
20-40岁 | |||
大于40岁 | |||
合计 |
（2）从购买意愿弱的市民中按年龄进行分层抽样，共抽取5人，从这5人中随机抽取2人进行采访，记抽到的2人中年龄大于40岁的市民人数为
，求的分布列和数学期望．
附：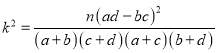
．
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 10.828 |
